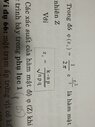How Many Type A Pigs Have 3 DYL Blood in a Herd of 1,000?

[Memo]

Mentor note: Thread moved from technical section to here, so is missing the homework template.
TL;DR Summary: The weight of DYL 3-blood hybrid pigs after correction of a farm is a random quantity with a normal distribution. Knowing that the probability of a pig weighing over 20 kg is 0.1587 and over 25 kg is 0.0228. If the pig weighs over 19 kg, it is called type A pig. How many type A pigs from the farm's herd of 1,000 pigs have 3 DYL blood?

Sample size=1000
P(x>20)=0.11857
P(x>25)=0.0228

 

[scottdave]

Hello,

Is this schoolwork? If so, did you read about using the homework templates? To get help with schoolwork, you need to show what you have tried, then we will guide you in the right direction.

 

[Memo]

Hello,

Is this schoolwork? If so, did you read about using the homework templates? To get help with schoolwork, you need to show what you have tried, then we will guide you in the right direction.

Sorry, I don't know where to start, I'm not familiar with this type of task. There's no sample mean the p(x=19) so I really don't know where to start. Please help me

 

[Mark44]

There's no sample mean

You don't need the sample mean, but you do need the population mean $\mu$ and population standard deviation $\sigma$. Are these given? If so the problem would be relatively easy to solve.

 

[Memo]

You don't need the sample mean, but you do need the population mean $\mu$ and population mean standard deviation $\sigma$. Are these given? If so the problem would be relatively easy to solve.

They're not given

 

[FactChecker]

Knowing that the probability of a pig weighing over 20 kg is 0.1587

That is exactly the probability of being over 1 standard deviation above the mean for a normal distribution.

and over 25 kg is 0.0228.

Can you find this probability in a standard normal table? If so, you can figure out what the standard deviation is. And then use my comment above to determine the mean.

If the pig weighs over 19 kg, it is called type A pig. How many type A pigs from the farm's herd of 1,000 pigs have 3 DYL blood?

Sample size=1000
P(x>20)=0.11857

That probability does not match the probability given above.

P(x>25)=0.0228

Ok.

 

[Memo]

That is exactly the probability of being over 1 standard deviation above the mean for a normal distribution.

Can you find this probability in a standard normal table? If so, you can figure out what the standard deviation is. And then use my comment above to determine the mean.

That probability does not match the probability given above.

Ok.

There's no table, the task only gives us the two proportions (as seen above) and the sample size.

 

[FactChecker]

There's no table, the task only gives us the two proportions (as seen above) and the sample size.

CORRECTION: Maybe this is about a binomial approximation to normal.
CORRECTION TO THE CORRECTION: This original post was probably what the problem wanted.
See post #6 and @scottdave 's post #14.

Why else would the problem state that it was a normal distribution? Without that, there is no unique answer. Don't you have a textbook and the usual probability tables? Is this for a class? In any case, you can find the standard normal tables on the internet.

 

[Memo]

Why else would the problem state that it was a normal distribution? Without that, there is no unique answer. Don't you have a textbook and the usual probability tables? Is this for a class? In any case, you can find the standard normal tables on the internet.

Sorry, my English isn't good. I thought you were asking about the dataset. I'm provided with the normal distribution but I don't see how it's gonna help

 

[Memo]

CORRECTION: Maybe this is about a binomial approximation to normal.
Why else would the problem state that it was a normal distribution? Without that, there is no unique answer. Don't you have a textbook and the usual probability tables? Is this for a class? In any case, you can find the standard normal tables on the internet.

You mean using the formula in the photo below? Could you tell me what to do next if I can search for the numbers?

 

[WWGD]

I'd say the 1-2-3, aka 68-95-99.7 rule of normal distribution should come in handy.

 

[Memo]

I'd say the 1-2-3, aka 68-95-99.7 rule of normal distribution should come in handy.

There's no population mean and SD

 

[WWGD]

There's no population mean and SD

True, but you can use the rule to find/approximate it.

 

[scottdave]

Your tables give the probabilities that something is less than the value. The problem gives probabilities of greater than (more than 20 kg, more than 25 kg). So you need to find the values (1 - 0.1587) and (1 - 0.0228) in the table.

How many Standard Deviations separate these two values? How many kilograms separate these two values? proceed from there.

I believe your p(>20) = 0.11587 is a typo: " probability of a pig weighing over 20 kg is 0.1587 "

 

[scottdave]

Learning how to read and understand a Normal table takes some practice. There is software and online tools that will churn out the values for you, but if you don't understand the proper inputs to give, then you will get nonsense answers.

For online tools, I like the following. It shows a picture of what it is calculating. https://davidmlane.com/hyperstat/z_table.html

 

[WWGD]

Learning how to read and understand a Normal table takes some practice. There is software and online tools that will churn out the values for you, but if you don't understand the proper inputs to give, then you will get nonsense answers.

For online tools, I like the following. It shows a picture of what it is calculating. https://davidmlane.com/hyperstat/z_table.html

Though symmetry about the mean of the Normal ( 0 for the Standard Normal) simplifies things quite a bit.

 

[Memo]

Learning how to read and understand a Normal table takes some practice. There is software and online tools that will churn out the values for you, but if you don't understand the proper inputs to give, then you will get nonsense answers.

For online tools, I like the following. It shows a picture of what it is calculating. https://davidmlane.com/hyperstat/z_table.html

Sorry, I don't really get what you were talking about, I've just learned about this topic like a week ago. I'm provided with 2 standard normal distribution tables (which use Probability density function and Cumulative distribution function) and multiple other tables (Binomial Probability Distribution, the Poisson distribution,...). Could you check if my answer is correct, thank you very much.

 

[WWGD]

Seems fine. But round down the number of pigs to 527 and let us have that .9 of a pig for the homework help.

 

[Memo]

Seems fine. But round down the number of pigs to 527 and let us have that .9 of a pig for the homework help.

what do you mean? Shouldn't I round the number?

 

[WWGD]

what do you mean? Shouldn't I round the number?

Just kidding, Memo ;). Edit: No need to round down.

 

[FactChecker]

I'm provided with 2 standard normal distribution tables (which use Probability density function and Cumulative distribution function)

That is all you need to answer this problem. Pay special attention to @scottdave 's post #14.

(PS. I should not have crossed out my answer in post #8. It was correct.)

 

[berkeman]

(PS. I should not have crossed out my answer in post #8. It was correct.)

You might still have time to add a comment in that post that mentions that it is actually correct (if not, I can do it for you). It's best not to alter older posts too much since it confuses readers later, but adding an editorial note should be fine.