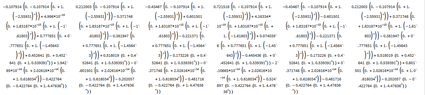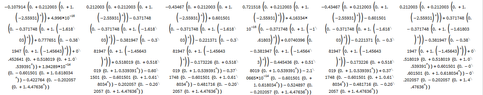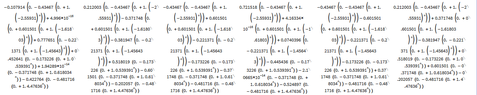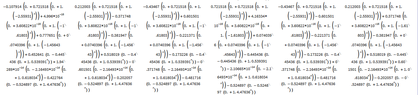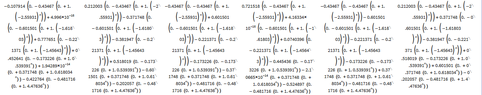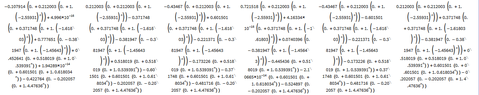How many walks of length $n$ can you find on this graph?

[Ackbach]

Here is this week's POTW:

-----

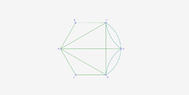
For the following graph, find the number of walks of length $n$ from any vertex to any other vertex. Use of technology is allowed (but explain what you did and how you did it).

https://www.physicsforums.com/attachments/4470._xfImport

-----

Remember to read the http://www.mathhelpboards.com/showthread.php?772-Problem-of-the-Week-%28POTW%29-Procedure-and-Guidelines to find out how to http://www.mathhelpboards.com/forms.php?do=form&fid=2!

 

[Ackbach]

No one solved this week's University POTW. Here is my solution.

Spoiler

First, you start with the adjacency matrix, where the $i,j$th entry in the matrix represents the number of paths from vertex $i$ to vertex $j$. Using Mathematica (really Wolfram Programming Cloud), I assigned this as follows:

A={{0.,1,1,1,1,1},{1,0,1,0,0,0},{1,1,0,2,1,0},{1,0,2,0,2,0},{1,0,1,2,0,1},{1,0,0,0,1,0}} ; A//MatrixForm

The result was

$$\begin{bmatrix}
0. &1 &1 &1 &1 &1 \\
1 &0 &1 &0 &0 &0 \\
1 &1 &0 &2 &1 &1 \\
1 &0 &2 &0 &2 &0 \\
1 &0 &1 &2 &0 &1 \\
1 &0 &0 &0 &1 &0
\end{bmatrix}$$

Because the graph is not directed, this matrix is by necessity symmetric, and therefore diagonalizable.

Further executing the steps

vecs=Eigenvectors[A]
Diag=Inverse[Transpose[vecs]].A.Transpose[vecs] //Chop;
Diag // Chop // MatrixForm

produced the diagonal matrix similar to $A$. Moreover, as a check,

Transpose[vecs].Diag.Inverse[Transpose[vecs]] //Chop //MatrixForm

produced $A$ back at me. Note that I introduced decimals to force Wolfram Programming Cloud to recognize the need for numerical computations. Unfortunately, the symbolic approach was far too unwieldy, as finding the eigenvalues involved solving a sixth-order polynomial - not even possible in principle.

Now for the crux of the matter. It can be shown that the $i,j$th entry of $A^n$ gives the number of walks of length $n$ from vertex $i$ to vertex $j$. Hence, this diagonalization is precisely what is needed to compute the $n$th power of $A$. If $D$ is the diagonal matrix similar to $A$ - that is, $A=P^{-1}DP$ for some invertible $P$ - then $A^n=P^{-1}D^n P$, and $D^n$ turns out to be exceptionally easy to compute. All we have to do is exponentiate the main diagonals, and then perform the matrix multiplication indicated to get $A^n$. The result was quite a challenge to display. First the code:

Transpose[vecs].MatrixPower[Diag,n].Inverse[Transpose[vecs]] //MatrixForm

I had to take six screenshots, one for each row, to get the full results to show up here on MHB. There is far too much text for a single post otherwise. Here they are:

View attachment 4489View attachment 4490View attachment 4491View attachment 4492View attachment 4493View attachment 4494

Once you've attained this result, it's not difficult to get the result for any particular $n$. Just execute (for $n=3$, say) the code

Transpose[vecs].MatrixPower[Diag,3].Inverse[Transpose[vecs]] //MatrixForm

and you'll get the correct result.