- #1
gallimaufry
- 6
- 0
lets say we have a balance with these masses attached:
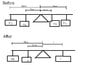
1) 11g mass at 7cm to the left of the fulcrum
2) 32g mass at 16cm to the left of the fulcrum
3) 11g mass at 7cm to the right of the fulcrum
4) 32g mass at 16 cm to the right of the fulcrum
This balance should be balanced right now because we have the same weights on each side. Let's say i wanted to combine the masses on the right so that i have one mass on the right balancing out the 2 masses on the left, How would i figure out what the mass is and the distance it should be at. I added a picture of the original balance to give you a visual, and another picture to show you what I want it to look like. In the picture the before and after should both be balanced, I just don't know what should go in the after picture. Thanks for the help.
1) 11g mass at 7cm to the left of the fulcrum
2) 32g mass at 16cm to the left of the fulcrum
3) 11g mass at 7cm to the right of the fulcrum
4) 32g mass at 16 cm to the right of the fulcrum
This balance should be balanced right now because we have the same weights on each side. Let's say i wanted to combine the masses on the right so that i have one mass on the right balancing out the 2 masses on the left, How would i figure out what the mass is and the distance it should be at. I added a picture of the original balance to give you a visual, and another picture to show you what I want it to look like. In the picture the before and after should both be balanced, I just don't know what should go in the after picture. Thanks for the help.