How much force does the 20 kg block exert on the 10 kg block?

[paulimerci]

Homework Statement

Assuming that the coefficient of friction between each block and the surface was 0.15, what would be the force of the 20 kg block pushing on the 10 kg block?

Relevant Equations

F= ma

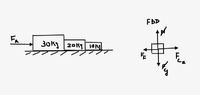
The contact force on 10 kg due to 20 kg is taken as Fc2
m1 = 30kg, m2 = 20kg, m3 = 10kg
F_A = Applied force
μ = 0.15

Net force = mass X acceleration
Fc2-Friction force = m3 X a, where a = F_A / (m1 +m2+ m3). Therefore the equation becomes
Fc2 = m3 F_A/(m1+m2+m3) + μN
= F_A/6 +15

I calculated acceleration taking all the blocks as one system. Does the expression above is correct or do I have to do any corrections?

 

[TSny]

Fc2-Friction force = m3 X a,

OK, if "friction force" is the friction force between m₃ and the surface.

where a = F_A / (m1 +m2+ m3).

No. Think about this. Is F_A the net horizontal force acting on the system?

 

[paulimerci]

OK, if "friction force" is the friction force between m₃ and the surface.No. Think about this. Is F_A the net horizontal force acting on the system?

The object doesn’t accelerate in the vertical direction, it accelerates only along the horizontal. The net force acting along Y would be the normal force and the force of gravity and they both cancel because they are balanced and the unbalance forces are along X, which is the force of friction and the contact force due to 20kg. Am I right?

 

[kuruman]

You are right for the vertical direction. The net horizontal force on the 3-mass system is the sum of F_A and the three friction forces acting on each mass. On the 20 kg mass, it is the sum of the forces from (a) the 30 kg mass, (b) the 10 kg mass and (c) friction from the surface.

 

[paulimerci]

You are right for the vertical direction. The net horizontal force on the 3-mass system is the sum of F_A and the three friction forces acting on each mass. On the 20 kg mass, it is the sum of the forces from (a) the 30 kg mass, (b) the 10 kg mass and (c) friction from the surface.

Thanks, Is it F_A -3 Friction force = (m1+m2+m3)a?

 

[TSny]

Is it F_A -3 Friction force = (m1+m2+m3)a?

Can you be more explicit? That is, can you write a mathematical expression for "3 Friction force"?

 

[paulimerci]

Can you be more explicit? That is, can you write a mathematical expression for "3 Friction force"?

sure,
Friction force for 30kg = F_A -m1a - Fc1
Friction force for 20kg = Fc1-Fc2-m2a
Friction force for 10kg = Fc2-m3a
adding friction force to the left = adding horizontal forces to the right, I get
Friction force = F_A/3 - (m1+m2+m3)a/3

 

[paulimerci]

sure,
Friction force for 30kg = F_A -m1a - Fc1
Friction force for 20kg = Fc1-Fc2-m2a
Friction force for 10kg = Fc2-m3a
adding friction force to the left = adding horizontal forces to the right, I get
Friction force = F_A/3 - (m1+m2+m3)a/3

So, substitute Friction force in the very first equation,
Fc2 = m3a + Force friction
= m3 FA/(m1+m2+m3) + F_A/3 - (m1+m2+m3)a/3
= F_A/6 + F_A/3 - F_A/3
= F_A/6
Have I done it right now?

 

[kuruman]

Have I done it right now?

No, try again. You have not used the coefficient of kinetic friction $\mu_k=0.15$ to find the force of kinetic friction. Why is it F_A/3 - (m1+m2+m3)a/3? Look up "kinetic friction."

 

[paulimerci]

No, try again. You have not used the coefficient of kinetic friction $\mu_k=0.15$ to find the force of kinetic friction. Why is it F_A/3 - (m1+m2+m3)a/3? Look up "kinetic friction."

I have to find answer in terms of F_A.
Is the expression for force of friction is wrong? If I substitute force friction as $\mu$ I'm not getting the answer.

 

[kuruman]

I have to find answer in terms of F_A.
Is the expression for force of friction is wrong? If I substitute force friction as $\mu$ I'm not getting the answer.

Yes, your expression is correct. I got confused about which mass is $m_3$. Sorry about that.

 

[paulimerci]

Yes, your expression is correct. I got confused about which mass is $m_3$. Sorry about that.

Thanks, Then do I really need to substitute for $mu$?

 

[kuruman]

Thanks, Then do I really need to substitute for $mu$?

If you do, it will drop out eventually because the force of friction is proportional to each mass by the same proportionality constant $\mu_k$. You would have to put it in if the coefficients of kinetic friction were different for each mass.

 

[paulimerci]

If you do, it will drop out eventually because the force of friction is proportional to each mass by the same proportionality constant $\mu_k$. You would have to put it in if the coefficients of kinetic friction were different for each mass.

You are correct, thank you!

 

[paulimerci]

You are correct, thank you!

In post # 1, I wrote acceleration = F_A/(m1+m2+m3), so when I calculate acceleration for the whole system and friction is also involved, the above equation will become acceleration = F_A - force friction/(m1+m2+m3). right?

 

[kuruman]

In post # 1, I wrote acceleration = F_A/(m1+m2+m3), so when I calculate acceleration for the whole system and friction is also involved, the above equation will become acceleration = F_A - force friction/(m1+m2+m3). right?

Not right. Let's put Newton's second together. The net force is
$F_{\text{net}}=F_A-f$ so $$(m_1+m_2+m_3)a=F_{\text{net}}=F_A-f\implies a=\frac{F_A-f}{(m_1+m_2+m_3)}.$$You must divide both forces by the sum of the masses.

Here is how you take friction into account correctly. I assume that the coefficient of friction is different between each mass and the table to make a point. In this case the total force of friction on the 3-mass system is $f=(\mu_1m_1+\mu_2m_2+\mu_3m_3)g$. Then $$(m_1+m_2+m_2)a=F_A-(\mu_1m_1+\mu_2m_2+\mu_3m_3)g$$ from which we find the acceleration $$a=\frac{F_A}{(m_1+m_2+m_3)}-\frac{(\mu_1m_1+\mu_2m_2+\mu_3m_3)g}{(m_1+m_2+m_3)}.$$Now Newton's second law for mass $m_3$ is
$m_3a=F_C-\mu_3m_3g \implies F_C=m_3a +\mu_3m_3g.$ We now put the expression for the acceleration to get $$F_C=\frac{m_3 F_A}{(m_1+m_2+m_3)}-\frac{m_3(\mu_1m_1+\mu_2m_2+\mu_3m_3)g}{(m_1+m_2+m_3)}+\mu_3m_3g.$$Noting that $m_1=3m_3$ and $m_2=2m_3$, this simplifies to $$F_C=\frac{F_A}{6}-\left(\frac{3\mu_1+2\mu_2+\mu_3}{6}-\mu_3\right)m_3g.$$The point I want to make after all this is that your method works only when the second term in the expression above evaluates to zero. For this to happen, one choice of coefficients is $\mu_1=\mu_2=\mu_3=\mu.$

 

[paulimerci]

Not right. Let's put Newton's second together. The net force is
$F_{\text{net}}=F_A-f$ so $$(m_1+m_2+m_3)a=F_{\text{net}}=F_A-f\implies a=\frac{F_A-f}{(m_1+m_2+m_3)}.$$You must divide both forces by the sum of the masses.

Here is how you take friction into account correctly. I assume that the coefficient of friction is different between each mass and the table to make a point. In this case the total force of friction on the 3-mass system is $f=(\mu_1m_1+\mu_2m_2+\mu_3m_3)g$. Then $$(m_1+m_2+m_2)a=F_A-(\mu_1m_1+\mu_2m_2+\mu_3m_3)g$$ from which we find the acceleration $$a=\frac{F_A}{(m_1+m_2+m_3)}-\frac{(\mu_1m_1+\mu_2m_2+\mu_3m_3)g}{(m_1+m_2+m_3)}.$$Now Newton's second law for mass $m_3$ is
$m_3a=F_C-\mu_3m_3g \implies F_C=m_3a +\mu_3m_3g.$ We now put the expression for the acceleration to get $$F_C=\frac{m_3 F_A}{(m_1+m_2+m_3)}-\frac{m_3(\mu_1m_1+\mu_2m_2+\mu_3m_3)g}{(m_1+m_2+m_3)}+\mu_3m_3g.$$Noting that $m_1=3m_3$ and $m_2=2m_3$, this simplifies to $$F_C=\frac{F_A}{6}-\left(\frac{3\mu_1+2\mu_2+\mu_3}{6}-\mu_3\right)m_3g.$$The point I want to make after all this is that your method works only when the second term in the expression above evaluates to zero. For this to happen, one choice of coefficients is $\mu_1=\mu_2=\mu_3=\mu.$

Thanks for the detailed derivation, For the acceleration of the system (#post 8) I didn't include friction force and I'm able to arrive at the correct answer

Not right. Let's put Newton's second together. The net force is
$F_{\text{net}}=F_A-f$ so $$(m_1+m_2+m_3)a=F_{\text{net}}=F_A-f\implies a=\frac{F_A-f}{(m_1+m_2+m_3)}.$$You must divide both forces by the sum of the masses.

Here is how you take friction into account correctly. I assume that the coefficient of friction is different between each mass and the table to make a point. In this case the total force of friction on the 3-mass system is $f=(\mu_1m_1+\mu_2m_2+\mu_3m_3)g$. Then $$(m_1+m_2+m_2)a=F_A-(\mu_1m_1+\mu_2m_2+\mu_3m_3)g$$ from which we find the acceleration $$a=\frac{F_A}{(m_1+m_2+m_3)}-\frac{(\mu_1m_1+\mu_2m_2+\mu_3m_3)g}{(m_1+m_2+m_3)}.$$Now Newton's second law for mass $m_3$ is
$m_3a=F_C-\mu_3m_3g \implies F_C=m_3a +\mu_3m_3g.$ We now put the expression for the acceleration to get $$F_C=\frac{m_3 F_A}{(m_1+m_2+m_3)}-\frac{m_3(\mu_1m_1+\mu_2m_2+\mu_3m_3)g}{(m_1+m_2+m_3)}+\mu_3m_3g.$$Noting that $m_1=3m_3$ and $m_2=2m_3$, this simplifies to $$F_C=\frac{F_A}{6}-\left(\frac{3\mu_1+2\mu_2+\mu_3}{6}-\mu_3\right)m_3g.$$The point I want to make after all this is that your method works only when the second term in the expression above evaluates to zero. For this to happen, one choice of coefficients is $\mu_1=\mu_2=\mu_3=\mu.$

Thank you, When friction force with different coefficients are involved the second term in the expression can't become zero.

 

[kuruman]

Thanks for the detailed derivation, For the acceleration of the system (#post 8) I didn't include friction force and I'm able to arrive at the correct answer

Right. My point is that if you don't include friction because you didn't have to for this particular problem, you might come to believe that you don't have to include friction for any problem. When the coefficients of friction are different, your method will give an incorrect result because it only works when the coefficients of friction are the same. I am pointing this out to make you aware of this pitfall. It is safer to find the general solution and then adapt it to the particular problem at hand than to generalize from the particular solution. That's all.