How Often Will I Meet the Mailman at the Same Mailbox?

[anorlunda]

I need help trying to model this true anecdote.

Every nice weather day, I like to climb a mountain. It takes a 40 minute drive to get there, 40 minutes climb up, 10 minute break at the summit, 30 minutes down, and 40 minutes drive home. 160 minutes total. On the way home, I repeatedly meet a mailman putting mail into the same mailbox. I'm surprised to meet the mailman at exactly the same mailbox as often as 25% of the trips. That 25% number seems unexpectedly high, so I want to model it.

I divide the trip into a chain of sequential discrete steps; say 160 steps. Step number i has a base time T_i plus a nonnegative random delay D_i. Random delays include traffic lights, stop signs, stopping to allow other people to pass on the trail, and reading my PF alerts during my break at the summit (sometimes posting answers).

The mailman has his own chain T_j + D_j. I presume the mailman's delays are statistically independent from my delays. I don't know the mailman's total trip time or his starting time.

My chain and the mailman's chain intersect at one specific mailbox location. The residence time in that location is 1 minute. That is depicted by this little diagram (if it had 160 dots). Blue is my chain, green is the mailman's chain, red is the intersection.

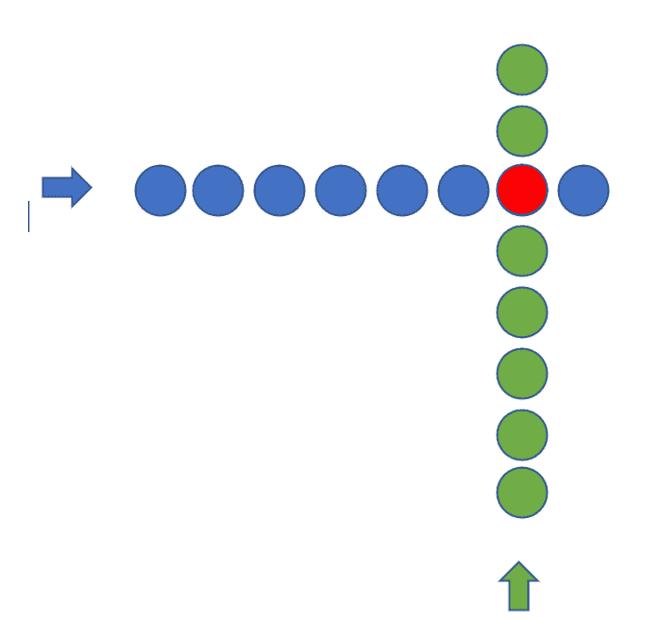
What is the probability of me and the mailman both occupying the red intersection in the same minute? That is what I want to model. Help would be appreciated.
Th\sumTi

 

[bob012345]

I've got a very very simple model that you can tear apart but please be kind. Assume there is a spread in minutes you pass by the mailbox of $n$. Assume there is one for the mailman of $m$. Then my model for the combined probability is this;

$$ p = \frac{1}{n} \frac{1}{m} (n+m)$$

If $n$= $m$ = 8 min then $p = 0.25$

 

[andrewkirk]

I find this problem easier to solve with a continuous model than with a discrete one.

Whether one sees the postman depends on two key random variables: the difference $U$ in time between his arrival and my arrival at that address, and the length of time $T$ that he spends at that address. I think $T$ will have far less variability than $U$, as $U$ depends on all the possible delays one can encounter en route. Since modelling both random variables would make the analysis much more complex, I'll propose a model that assumes $T$ to be constant.

Assume the postman's and my arrival time at the address are $P$ and $J$ respectively, and assume that I see the postman if the difference in arrival time, $U=J-P$, lies in the range $[a, b]$. Measure time in seconds since midnight. We will probably have $a<0<b$. For instance if $[a,b]=[-50, 20]$ I will see the postman at that address if he arrives between 50 seconds before me and 20 seconds after me.

Then we can calculate the probability of seeing the postman at that address as:
$$Pr(J - P\in [a,b])=Pr(U\in [a,b]) = F_U(b)-F_U(a)$$
where $F_U(y)$ is the cumulative distribution function (CDF) of random variable $U$ - ie probability that $U<y$.

In the absence of any other information about distributions, one often assumes them to be normal (Gaussian), which simplifies the calculations. So let's assume $P\sim \mathscr N(\mu_P, \sigma_P{}^2)$ and $P\sim \mathscr N(\mu_J, \sigma_J{}^2)$. We'll also assume $J$ is independent of $P$. That assumption is dodgy by the way since bad weather will probably delay us both. We can enhance the analysis later if we want to take account of a dependence that recognises that.

Since independent normal distributions add in a nice manner, that gives us $U\sim \mathscr N(\mu_J - \mu_P, \sigma_J{}^2+\sigma_P{}^2)$. So the probability of seeing the postman will be:
$$F_U(b) - F_U(a) =
\Phi\left(\frac{b-\mu_U}{\sigma_U}\right)
- \Phi\left(\frac{a-\mu_U}{\sigma_U}\right) =
\Phi\left(\frac{b-\mu_U}{\sqrt{\sigma_J{}^2+\sigma_P{}^2}}\right)
- \Phi\left(\frac{a-\mu_U}{\sqrt{\sigma_J{}^2+\sigma_P{}^2}}\right)
$$
where $\mu_U=\mu_J-\mu_P$ and $\Phi$ is the CDF of the standard normal distribution, which function is built into any serious mathematical calculation system.

To calculate the probability, you need to make assumptions about:
- the limits $[a,b]$ of the range of the difference in arrival times that would allow you to see the postman at the address;
- the mean $\mu_U$ of the difference in arrival times; and
- the standard deviations $\sigma_P,\sigma_J$ of the arrival times of you and the postman. These will be affected by the potential for both delays in starting the trips and delays en route.

 

[bob012345]

Perhaps it should be this

$$p =\frac{1}{2} \frac{1}{n} \frac{1}{m} (n+m)$$ so if both are 1 that means a perfect schedule and p=1.

But I was only trying to get the ball rolling...

 

[berkeman]

On the way home, I repeatedly meet a mailman putting mail into the same mailbox. I'm surprised to meet the mailman at exactly the same mailbox as often as 25% of the trips. That 25% number seems unexpectedly high, so I want to model it.

Please post the following data for the last few months of this happening, so we can analyze the data:

For each day:
** The date and day of the week
** The time you left home
** The time you passed that mailbox on your way back home
** Whether you saw that mail delivery person that day

On the face of it, the coincidence would probably just be a time coincidence. I'd also ask you to talk to that mail carrier to find out what their normal route days and times are, but that would probably just creep them out more since they keep seeing you driving by casing their route over and over again...

 

[bob012345]

I don't think this is that mysterious since you and the mailman are on fixed routes and probably similar schedules. There would be a 100% chance your paths cross somewhere and the actual range is going to be limited so a 25% hit rate within that limited window does not seem extraordinary to me.

My suggestion is to try and set up a simple Monte-Carlo simulation so you don't have to figure probabilities a priori and tabulate the hit rates at the mailbox.

 

[bob012345]

Any progress?

Reminds me of when I used to frequent a local bookstore, almost every time I showed up there was this guy, not an employee, always there. This went on for years. I could only conclude he was there a lot more than me since my times were not that regular.

 

[anorlunda]

Any progress?

Reminds me of when I used to frequent a local bookstore, almost every time I showed up there was this guy, not an employee, always there. This went on for years. I could only conclude he was there a lot more than me since my times were not that regular.

Yeah, I did run a Monte Carlo as you suggested. After 10000 trials, I found mailbox meetups:
min,max,avg, std= 5 18 10.38 3.0 all in percent of trials.

That was with a 1 minute window of me and the mailman meeting. But changing that to 30 seconds, yielded.
min,max,avg, std= 5 18 10.38 3

So 5% is lower than my subjective guess of 20%, but not wildly different. However, the most critical parameter is the size of the time window to declare as a meetup.

So, what did I learn? The KISS principle applies. The simplest solution, a Monte Carlo trial, showed that more complex methods were unnecessary.

Thanks for the push in the right direction.

 

[bob012345]

Yeah, I did run a Monte Carlo as you suggested. After 10000 trials, I found mailbox meetups:
min,max,avg, std= 5 18 10.38 3.0 all in percent of trials.

That was with a 1 minute window of me and the mailman meeting. But changing that to 30 seconds, yielded.
min,max,avg, std= 5 18 10.38 3

So 5% is lower than my subjective guess of 20%, but not wildly different. However, the most critical parameter is the size of the time window to declare as a meetup.

So, what did I learn? The KISS principle applies. The simplest solution, a Monte Carlo trial, showed that more complex methods were unnecessary.

Thanks for the push in the right direction.

The numbers look the same for 30 seconds? Typo?

 

[anorlunda]

The numbers look the same for 30 seconds? Typo?

Whoops, yes typo. And now I lost the window to copy from. But in rough numbers, with a 30 second window were min,max,avg=1, 10, 2