- #1
Omar Nagib
- 4
- 0
An ideal Carnot engine is composed of two reservoirs and a working fluid. The hot Reservoir and the cold one have temperatures ##T_1## and ##T_2## respectively, with ##T_1>T_2##. The working fluid is in a phase transition and has temperature ##T_1## at the start of the Carnot cycle. It undergoes another phase transition at ##T_2## at the end of the cycle to return to its original state.This is a P-V diagram of the Carnot cycle which proceeds in fours steps:
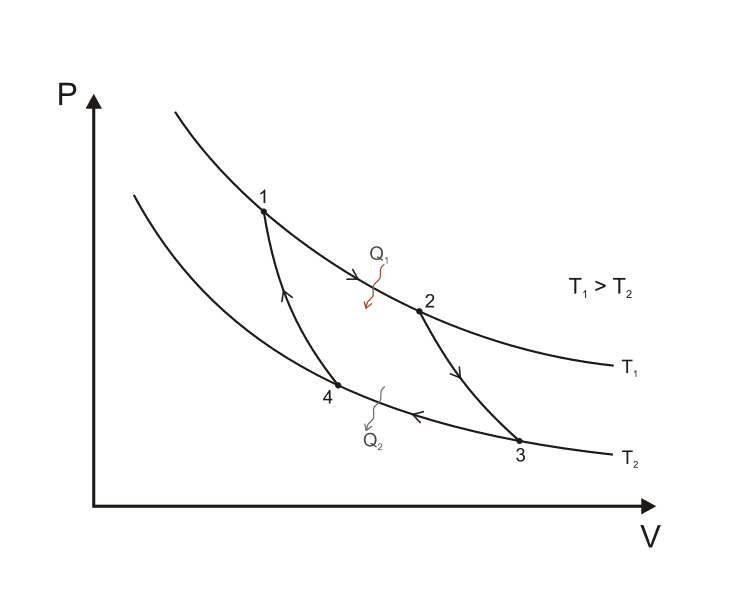
I'm particularly interested in the two stages (from 1 to 2) and (from 3 to 4). They can be described as follows:
1) Stage (from 1 to 2) is an reversible isothermal expansion of the working fluid to transform from the liquid state to the gaseous one. The working fluid is at ##T_1## and it happens to have boiling point at ##T_1##; Hence heat ##Q_1## is supplied to the fluid from the hot reservoir until it transforms to a gas keeping its temperature constant along the whole process.(that the fluid's temperature is constant during the whole process is owing to it being in a phase transition).
2) Stage (from 3 to 4) is an reversible isothermal compression, and its similar to what we have just described, with the difference being in this case, heat ##Q_2## is drawn out of the fluid and transfers to the cold reservoir and the fluid transforms from gas to liquid retaining a constant temperature of ##T_2## throughout the whole process
I'm puzzled by the mechanism by which the working fluid undergoes phase transition. So at stage (from 1 to 2), both the fluid and the hot reservoir have the exact temperature, so that they're in a thermal equilibrium; Hence there should be no heat or energy exchange between the two bodies. The same can be said of stage (from 3 to 4).
So how is it possible for heat to flow from two bodies having the exact same temperature?
I'm particularly interested in the two stages (from 1 to 2) and (from 3 to 4). They can be described as follows:
1) Stage (from 1 to 2) is an reversible isothermal expansion of the working fluid to transform from the liquid state to the gaseous one. The working fluid is at ##T_1## and it happens to have boiling point at ##T_1##; Hence heat ##Q_1## is supplied to the fluid from the hot reservoir until it transforms to a gas keeping its temperature constant along the whole process.(that the fluid's temperature is constant during the whole process is owing to it being in a phase transition).
2) Stage (from 3 to 4) is an reversible isothermal compression, and its similar to what we have just described, with the difference being in this case, heat ##Q_2## is drawn out of the fluid and transfers to the cold reservoir and the fluid transforms from gas to liquid retaining a constant temperature of ##T_2## throughout the whole process
I'm puzzled by the mechanism by which the working fluid undergoes phase transition. So at stage (from 1 to 2), both the fluid and the hot reservoir have the exact temperature, so that they're in a thermal equilibrium; Hence there should be no heat or energy exchange between the two bodies. The same can be said of stage (from 3 to 4).
So how is it possible for heat to flow from two bodies having the exact same temperature?