How Should I Find Limits for Variables u and v in Calculus?

[etf]

Hi!
Here is my task:

Here is my attempt of solution:

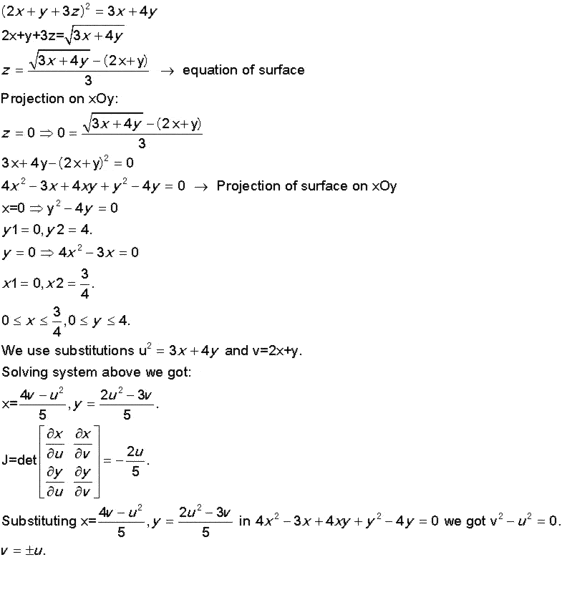
Does it make sense? How should I find limits for u and v?
I appreciate any help!

 

[Simon Bridge]

The task is:

Find the volume of the solid bounded by $(2x+y+3z)^2=3x+4y$ in the first octant.

You method was to solve the equation above for z (taken as height above the x-y plane) - you used a substitution, and then found the Jacobean, basically changing coordinate axis.

You have the new integrand z(u,v) - as the upper bound of the volume to be found.

Now you want to slice the volume parallel to the z-u axis.
The volume of the slice at position v, thickness dv, will be $$\renewcommand{\d}{\text{d}} \d V=\d v \int_{f(v)}^{g(v)}z(u,v)\d u$$

So the question becomes: what determines the upper and lower bounds of each slice?

 

[etf]

Thanks for reply!
I'm not sure I can answer...
I don't know limits of integration in x-y plane, that's problem. If I know that I could easily find limiits in u-v plane.

 

[Simon Bridge]

Oh right - in the x-y plane the lower limits would be 0, and the upper limit would be defined by the curve where z(x,y) intersects the x-y plane. The trouble is that you need to find, say, limits of x from 0 to f(y) ... where f is a function of y alone ... which is quite difficult from the expression. This is why you change the coordinates around: so the limits in the u-v axes are findable.

So:
Draw axis u vs v.

You know x>0 ... that should give you some relationships for u and v ... it may tell you that u<a: a is some number ... so you draw a line u=a ... all the u values are less than that. You may find that u<f(v) or v>f(u) ... so sketch the curve for that function etc.

Do it again for the limit y>0.

And again for the curve where z(u,v) intersects the u-v plane.

Once you have all those lines, you should be able to shade in the region you are doing the integration over.
Now you should be back on familiar territory.

It may be that your choice for u and v transformations is not good for this - if so, you need to find another transformation that works better.

 

[etf]

Something like this?

Here is graph:

 

[Simon Bridge]

That's the sort of thing - shade in the u-v plane regeon that corresponds to the region you are integrating over and the next step should be apparent.

you have $$v_1 > \frac{u^2}{4}, v_2<\frac{2u^2}{3}, v_3<u$$ ... blue, dashed, and red lines respectively.
your graph is v vs u - good choice - you want to shade the area between the two parabolas that is also under the line.

 

[etf]

Is it correct?

 

[Simon Bridge]

It looks like what I'd do... you've certainly got the right idea.
Well done.

 

[etf]

I would not have succeeded without your help.
Thanks a lot!

 

[Simon Bridge]

No worries.
You'd have got there eventually - you'd actually done all the calculations already ;)
Hopefully, you now have a better general feel for these integrals where, before, there was just these magic rules and formulas.
Cheers :)

On another note: it must have been a bit of a pain making and uploading those images.
Recommend you learn to use the LaTeX system - used in a lot of sites, also professionally and academically.
https://www.physicsforums.com/showpost.php?p=3977517&postcount=3
... it also helps preserve the answers for other people: notice i was careful to retype everything that would have the question make sense even if the pics vanished sometime later?

 

[etf]

I should definitely learn LaTeX, upload of images is really painful.

 

[Simon Bridge]

Use the quote button on any of my posts with an equation in them to see what I did.
Compare with the notes in the link.

It's well worth it - and not all that much trouble: the basics of typesetting equations takes about 10mins.
Most of the commands are pretty much what you'd guess... like if you want to write a sine function you type "\sin", you want a Greek letter you just write the name of it so I can write: "y=A\sin\omega t", to get $y=A\sin\omega t$ when I put it inside double-hash marks. Want a cap greek letter? Spell it with a cap: "\Omega" gets you $\Omega$.

It's faster, and easier even, than using wysiwyg equation editors ;)

Anyway - enjoy.