How Should Significant Figures Be Determined Without Numerical Data?

[SweatingBear]

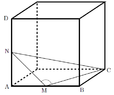
I received an excellent question about significant figures when there is no actual numerical data given. In the figure below, we have a cube circumscribing a triangle and the task is to find the angle at M. N and M are midpoints of the cube's side.

View attachment 1016

By using the Pythagorean theorem a few times and ultimately law of cosines, one can arrive at

\(\displaystyle \cos (\text{M}) = \frac { \frac 94 - \frac 12 - \frac 54 }{ -\sqrt{\frac 52} } \, ,\)

where one solution is \(\displaystyle M \approx 108.4349488^\circ\). Here is the problem: How many significant figures ought one to have for the angle? We were not given any numerical data, so what ought one to do? Integral values seems to be a natural, conventional practice; however, in terms of significant figures, the questions becomes much more interesting.

 

[Ackbach]

Re: No data; sig figs?

Couple of questions/comments:

1. Is $M$ the midpoint of $AB$? And is $N$ the midpoint of $AD$?

2. If you can give the exact answer, that would be preferable. A decimal approximation can also be useful - I'd probably just go to the tenth decimal place for precision.

 

[I like Serena]

Re: No data; sig figs?

In this case it's up to you how many digits you use.
In mathematics you're supposed to give an exact answer.
It's extra to provide an approximation.

My answer would be \(\displaystyle \text{M} = \arccos \big(-\frac 1{ \sqrt{10}}\big) \approx 108.4^\circ\).
I would include 1 digit after the decimal point only to indicate it is not exactly 108 degrees.If you're working with real measurements, as a rule of thumb, the approximation in the final answer should have the same total number of digits as the least significant measurement you used.
Note that any intermediate results should have at least 1 digit extra and preferably more.

 

[SweatingBear]

Re: No data; sig figs?

Couple of questions/comments:

1. Is $M$ the midpoint of $AB$? And is $N$ the midpoint of $AD$?

2. If you can give the exact answer, that would be preferable. A decimal approximation can also be useful - I'd probably just go to the tenth decimal place for precision.

1. Yes correct. Sorry about that, I forgot to write that in my first post.

2. All right, thank you!

In this case it's up to you how many digits you use.
In mathematics you're supposed to give an exact answer.
It's extra to provide an approximation.

My answer would be \(\displaystyle \text{M} = \arccos \big(-\frac 1{ \sqrt{10}}\big) \approx 108.4^\circ\).
I would include 1 digit after the decimal point only to indicate it is not exactly 108 degrees.If you're working with real measurements, as a rule of thumb, the approximation in the final answer should have the same total number of digits as the least significant measurement you used.
Note that any intermediate results should have at least 1 digit extra and preferably more.

Thanks, much appreciated.

 

[topsquark]

Re: No data; sig figs?

Here is the problem: How many significant figures ought one to have for the angle? We were not given any numerical data, so what ought one to do? Integral values seems to be a natural, conventional practice; however, in terms of significant figures, the questions becomes much more interesting.

As a Physicist who is known for his very, very bad lab data I usually assume a standard error of about 10%. (By comparison any competent lab student probably works at around a 5% standard error. And a professional somewhere lower than that...certainly less than 1% depending on the equipment.) Anyway if I have no idea about the uncertainty of the number I would normally guess at between 5% and 10%.

-Dan

 

[I like Serena]

Re: No data; sig figs?

As a Physicist who is known for his very, very bad lab data I usually assume a standard error of about 10%. (By comparison any competent lab student probably works at around a 5% standard error. And a professional somewhere lower than that...certainly less than 1% depending on the equipment.) Anyway if I have no idea about the uncertainty of the number I would normally guess at between 5% and 10%.

-Dan

Heh.
Suppose you had to measure an angle of about 108.4 degrees in a drawing.
How accurately would you measure it, say, for lab work?

 

[topsquark]

Re: No data; sig figs?

Heh.
Suppose you had to measure an angle of about 108.4 degrees in a drawing.
How accurately would you measure it, say, for lab work?

(snorts) With calipers I can get about a decimal point for accuracy. For precision on the other hand... Kablooey!

Let's put it this way. I once did the Millikan Oil Drop experiment. It's basically Physics hazing for Junior and Senior Physics lab students. (Some details on the internet.) It's an experiment to measure the charge on an electron. My answer for the charge of the electron? \(\displaystyle 1.6 \times 10^{19}\) C. I want you to look carefully at this well checked result...this is what my data told me.

Look at my result again. Let me compare it to the actual value for the charge on the electron: \(\displaystyle 1.6 \times 10^{-19}\) C. Note the difference? There is a -19 on the actual charge and a +19 on my result.

Yes, my answer was 38 orders of magnitude off. Using my result the orbit of the electron about a Hydrogen nucleus is on the order of the size of the orbit of Jupiter.

I now try to be generous about the standard error I attribute to my data.

-Dan