How Should the Magnetic Fields from Two Wires Combine at Point L?

[Puchinita5]

Homework Statement

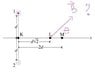
I upploaded a picture of the problem...

The part I'm stuck on asks this:
Point L is located a distance d sqrt2 from the midpoint between the two wires. Find the magnitude of the net magnetic field BL created at point L by both wires.


I had already solved that magnetic field produced by ONLY wire 1 at point L,
and found it to be (μI)/(2pid√3)

I realize that the magnetic field from wire 1 would be pointing up and to the right, whereas the magnetic field from wire 2 would point down and to the right. Therefore, I need to find the x component of the magnetic field and multiply by 2...

this is where I'm not understanding...so i took my previous answer, (μI)/(2pid√3), and figured i needed to multiply by cos theta, theta being the angle between the magnetic field and the x axis, in order to get the x component. This would be (d√2)/(d√3)...which doesn't give me the right answer...

I looked up the answer to this problem, and i see that they multiplied my answer by the SIN of theta, or d/(d√3)...but WHY?!

So i think the answer should be (μI√2)/(3dpi), but the correct answer is (μI)/(3dpi)

if anyone can tell me where my logic is wrong, i would greatly appreciate it because now I'm really confused! (and really frustrated LOL)

Homework Equations

The Attempt at a Solution

 

[rl.bhat]

In the triangle formed by the wires and point L, the angle defined by is the angle between the line joining the two wires and the line joining the wire and the point L. In that case cos θ = ...?

 

[Puchinita5]

i'm not quite sure what you mean...i edited the photo attachment to show what I'm thinking of with theta and the magnetic field... ?

 

[rl.bhat]

i'm not quite sure what you mean...i edited the photo attachment to show what I'm thinking of with theta and the magnetic field... ?

In the attachment join 1 and L. This line is perpendicular to B. The angle θ shown in the figure is the same as the angle between the line joining the two wires and the line joining 1 and L. In that case cosθ = d/d*sqrt3.