How to Approach the Prandtl Boundary Layer Equation for Steady Laminar Flow?

[sakif]

Homework Statement

Prove the following statement

Relevant Equations

Prandtl boundary layer equation for a two dimensional steady laminar flow of incompressible fluid over a semi infinite plate

I have tried to approach in the following way

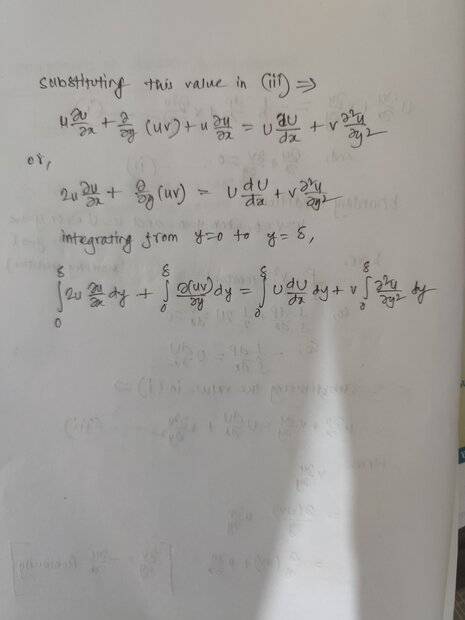
I am stuck. How should I approach this next.please help

 

[Arjan82]

I see you try to use the Bernoulli equation. But that is never going to work since that equation is only valid for inviscid flow. And in an inviscid flow no boundary layer can exist.

 

[Chestermiller]

I see you try to use the Bernoulli equation. But that is never going to work since that equation is only valid for inviscid flow. And in an inviscid flow no boundary layer can exist.

Far from the boundary, in the free stream, it is valid to use the Bernoulli equation. That's what boundary layer theory is all about.