- #1
msn009
- 53
- 6
For illustration purposes, I have attached an image of the line with the angle that I want to calculate. I am trying to determine the angle of rotation and the calculation that I am using currently is as below:
angle = math.atan2(y,x)
I use this formula to calculate the rotation for A and A', and then I add up the angle of a and b get the rotation. So I am really not sure if this is the correct way to do this. The idea in the end is to see if the rotation from A to A' is >70 degrees or <70 degrees. Sorry my math is pretty rusted at the moment.
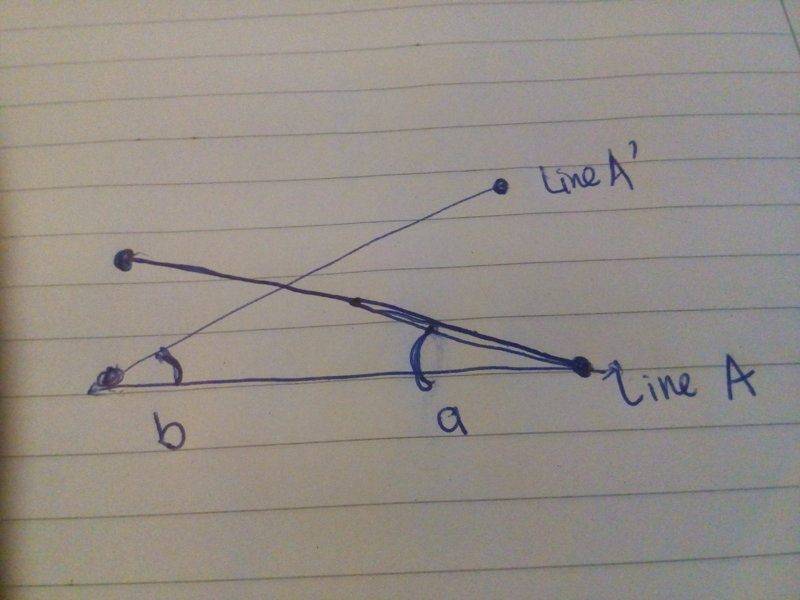
angle = math.atan2(y,x)
I use this formula to calculate the rotation for A and A', and then I add up the angle of a and b get the rotation. So I am really not sure if this is the correct way to do this. The idea in the end is to see if the rotation from A to A' is >70 degrees or <70 degrees. Sorry my math is pretty rusted at the moment.
