- #1
antonima
- 28
- 0
Hello physics forums,
I am writing a paper and I am wondering how to calculate the entropy of mixing in a two dimensional system. I am sure that entropy increases with mixing in a two dimensional system, but I do not know what equation to use. Would I just use the same equation as for 3-d systems?
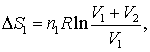
In which case V (volume) should be replaced with A (area) .. and R would be removed altogether to become
ΔS=S1*ln((A1+A2)/A1)
Is this right? I would appreciate any help. I don't think it would be very scientific if I just said 'the entropy of the system surely increases when size increases'...
I am writing a paper and I am wondering how to calculate the entropy of mixing in a two dimensional system. I am sure that entropy increases with mixing in a two dimensional system, but I do not know what equation to use. Would I just use the same equation as for 3-d systems?
In which case V (volume) should be replaced with A (area) .. and R would be removed altogether to become
ΔS=S1*ln((A1+A2)/A1)
Is this right? I would appreciate any help. I don't think it would be very scientific if I just said 'the entropy of the system surely increases when size increases'...