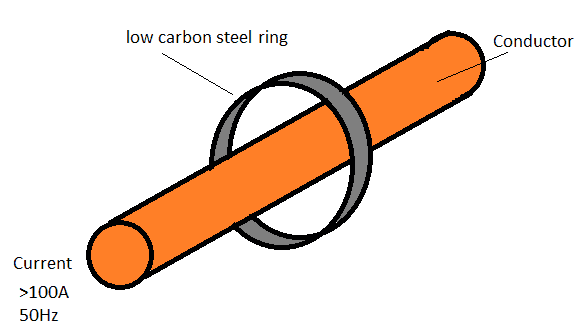
All you have stated so far are some dimensions and low-C Steel.
Steel is a metal alloy much like Curry is a mixed bag of spices. There is a wide range of materials under the same name, not just Fe and C.
"Mild" steel is mostly iron, Fe arranged in random atomic crystals with low carbon, C which can yield high permeability but with a 100:1 wide range on conduction losses from high resistance due to lack of molecular grain orientation of conductor electrons. Alloys Cr, Ni, Mb, Cu, O2, and other trace elements, affect the crystal lattice structures. Also, processing affects electrical loss greatly with how it was annealed, cold rolled or printed as well as the conductor thickness/skin depth ratio.
Each variable affects the mechanical, electrical, magnetic, thermal, and corrosive properties widely.
Although you are only interested in the magnetic, conductive and inductive properties of this 40mm thin ring, keep in mind the wide range of permeabilities, and conductance losses of steel make this impossible to predict without these metallurgical values.