How to calculate the force needed to get out of bed?

[CWatters]

Think that was what I said in #24.

The peak torque or force is the same. The work done is greater.

 

[marciokoko]

Ok and why is the work done greater? Is it simply because the "distance" covered is now 90 degrees + 20 = 110 degrees total?

Or does the inclination or something else have anything to do with it?

IOW, does it take the same amount of work from degree -20 to degree 0 as it does from degree 0 to degree 20?

 

[sophiecentaur]

Ok and why is the work done greater? Is it simply because the "distance" covered is now 90 degrees + 20 = 110 degrees total?

Or does the inclination or something else have anything to do with it?

IOW, does it take the same amount of work from degree -20 to degree 0 as it does from degree 0 to degree 20?

Why do you want to treat this in such an arm waving way? If you tried to treat your finances in this way you would soon end up with no money. It's fairly elementary mechanics and you should just do the proper sums. It's not a matter of 'opinion' and 'the way its put'; it's just a straightforward calculation.

 

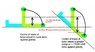
[marciokoko]

Sophie,

If its a straightforward calculation to calculate the difference between getting up from an incline of -20 vs from a 0 degree flat board, then what is that simple calculation? Can you show me?

 

[sophiecentaur]

A question that's well formed will often almost answer itself (that's a comment frequently made on PF).
If you draw a diagram of exactly the situation that you are interested in and mark the forces involved, you can use the few basic 'statics' equations (such as the principal of moments and the definition of Work) to tell you what you want.
In the case of getting up out of bed, the model needs to be drastically simplified if you want to get anywhere. Say exactly what the before and after situations are and you can determine the Work done. (mgh would be a start, where h is the height by which your cm is raised).
Whatever you do and to whatever level you want the analysis, you have to specify the problem. Only the questioner can do that (with a bit of guidance, possibly). So start at the very beginning and build ( that means draw, probably) a model to describe the question. . . . . . . . .

 

[marciokoko]

Ok perhaps I need to clarify. I am not a student, I am a curious person who a few days ago visited a museum where they had a house that was not flat, but rather inclined 20 degrees. So they take you through different rooms to show scenarios of what things change now that the house is inclined 20 degrees. They have a pool table and a table with chairs and the last room is a bedroom. They make you lie down on the bed and try to get up. Of course its impossible to get up from a -20 degree inclined bed.

I asked the guide what would be the physical concept that explained what changes from getting out of a normal bed vs this one with an incline? He was unable to explain it to me. So here I am, a 40 yr old adult who took physics but barely remembers anything anymore. So first let me clarify that I am not being lazy or cheating on my homework :-). I am simply trying to understand (without a high degree of mathematical precision) what changes when getting out of a flat be vs an inclined bed.

Yes of course the first thing I did was make a drawing and I posted it here at the beginning of the thread. The first thing I am trying to understand is simply, "why is it harder to get up out of the inclined bed"? Does the force needed to lift a weight at an angle increase? Or is the force the same but the work required different because that body is being lifted through a greater amount of degrees (-20 -> 90 vs 0 -> 90)? Or what, if anything else, is making it more difficult to get out of the inclined bed?

To be honest I got even more confused thinking that perhaps the force is still the same but the angle makes it more difficult. Then I realized I wasnt really clear about my concepts. So its not so much that I am interested in the exact mathematical calculation. I would like to start by first understanding what is making the "getting up" more difficult.

Thanks

 

[OmCheeto]

... Of course its impossible to get up from a -20 degree inclined bed.
...

Well, I'm not about to build a bed to prove you wrong, so please take a look at the following video, starting at t = 1:10 and ending at t = 1:20.

​

The guy in video does not look like a super hero, and is able to do a full sit-up from vertical.
So it would appear that the impossibility of getting out of an inclined bed is not based on physics.
My guess is, that you are still not properly describing the problem.

 

[marciokoko]

Thats because his feet arent moving because they are being held by a strap I guess.

I don't know how you sleep, but I surely don't strap my feet to the bed :-)

 

[CWatters]

Sorry, I've been away for a few days..

Ok and why is the work done greater? Is it simply because the "distance" covered is now 90 degrees + 20 = 110 degrees total?

Yes. In simple terms..

Work = Torque * Angular Displacement

That's the rotational equivalent of the linear..

Work = force * distanceAside: In this case the torque isn't constant so you need slightly more complex maths then this but it should give you the basic idea.

 

[sophiecentaur]

Yes of course the first thing I did was make a drawing and I posted it here at the beginning of the thread.

The reason that you are still finding it hard to solve this satisfactorily, is that your initial diagram, in fact, doesn't contain all the necessary information. The original question is wide open and can have many different answers. The goal posts in the thread keep changing and it would be better to specify just one particular question, relating to one, fully defined situation and then we / you could come up with an answer.
The trouble with Physics is that (classical Physics, at least) is very formal and has just one answer per situation. It's tiresome for people who 'just want an answer' because it seems to them that people are 'just' being smartness and picky. It really isn't the case (usually on PF, at least). The thread title is very hard to suss out; which Force and where applied - for instance?

 

[marciokoko]

Ok I'll try to be as clear and singular as possible. My first question is:

What physical phenomena makes it more difficult to get out of a 20 degree inclined bed vs a flat bed. (without your feet being tied or strapped or held)

 

[jose gonzales]

Since E=mc^2, getting out of bed requires the energy from 1 muffin and 2 cups of coffee.

 

[sophiecentaur]

You clearly know what you want to be told (or at least, you think you do). What do you actually mean by "get out of"? How do you specify the height of your inclined bed? Is one end raised above the horizontal reference or is the other end lowered? Are you just referring to 'sitting up', so your torso is vertical or are you expecting to stand up too? How are you assessing the 'difficulty' of getting up"? Is it maximum muscular effort or is it just to do with the mechanical work involved? All these questions (and more) need to be answered before you can hope to get an answer to your question. It really isn't that simple.
There are some partial answers that could be arrived at - for instance the work involved in getting your torso horizontal would need to be added to the work in getting from horizontal to vertical. That's just because the cm of your torso is lifted through a greater distance. But, of course, if the mean height of the mass being lifted is different, this will affect the work needed. Are you allowed to use your legs to help you; if you raise them first and then let them drop, you can make getting up 'easier' although the actual work done may be the same.
You need to break down the process into separate actions and specify each one in detail. Earlier in the thread there was discussion about gym equipment. How relevant is all that to your question? I know people with little legs and a massive torso, who could never get up in the way that people seem to be assuming in this thread. They have to roll over and use there arms, along with a lot of grunting. I could sympathise with them if they just stayed there.

 

[sophiecentaur]

Since E=mc^2, getting out of bed requires the energy from 1 muffin and 2 cups of coffee.

It all works by gravity - the gravity of the situation if you don't get up and go to work.

 

[valent]

I know from physics 101 that f = ma. And if I want to lift an object straight up i have to multiply its mass times gravity (acceleration) and I get the force I need to require to overcome it.

But what about lifting your body out of bed? Just the part where you physically get up from the lying down position to the sitting up position. In other words, just for lifting your torso up from horizontal to a vertical?

I know it has something to with the the angle but I am not sure how to incorporate it into f=ma.

Thanks

 

[marciokoko]

Ok, let me be clearer...

Here are the scenarios I am trying to compare, in order to understand why it was so difficult for me to get out of the inclined bed.

Im only interested in the part of getting out of bed that involves the "sitting up part". The person is lying down on a flat bed, tries to sit up without "pumping" his legs and not having anybody or anything holding his ankles. Specifically this refers to the raising of the torso from flat to vertical = 90 degrees.

Then i would like to compare that with having the same body on a bed which is inclined -20 degrees where the head is dipped lower than the feet.

In comparing those 2 situations I want to understand what makes it more difficult to get up from the inclined bed. At one moment I thought it was simply the fact that the torso was swinging 90=20=110 degrees. But intuition tells me it can't just be that, because if the bed were flat, sitting up the torso from a flat 0 degrees to 90 and then 20 degrees more towards the feet, is not as hard.

Right?

 

[abrogard]

Could it be that you're kidding yourself?

You feel it is harder to get sat up from 'head down' than from supine and I'll grant you that it certainly seems to be so when we try it.

But isn't that only because we don't reach a position of 'rest' against the force of gravity until we've moved that extra 20 degrees?

i.e. we just have to move further to get properly 'sat up' - which really means in a position where gravity is acting down along the body, doesn't it? Where we don't need any conscious muscle tension to maintain a comfortable position.

We have to move 110° before we can 'relax' and, in fact, we wouldn't be properly relaxed even then because the body would be slightly imbalanced and gravity still pulling on us. We need muscle tension in the abdomen to retain the position. Try it.

And during the course of that 110° we need to do a greater proportion of the work against the definite hard pull of gravity. Whereas when sitting up from supine we've only got about, what, 70°, of hard work and the last 20° is fairly effortless, the job's done. That's a ratio of 2:7. When starting from head down 20 ° we've got a ratio of 2:110 - and the final position, as I said, is still uncomfortable.

And lastly, sitting up in bed simply isn't as easy as we tend to think. We only do it once a day, mainly, and possibly help ourselves with little twists and manipulations here and there without even realising it. So we think it's easy.

Ask someone to practice a few 'sit up in bed' exercises and you're quickly into something quite strenuous, even to where it can damage people with abdominals in poor shape.

So maybe when it is all considered it simply isn't harder to sit up from head down, it just appears so, but it's really no harder than one would sensibly expect if one were aware of the whole situation.

All the physics gurus here seem to be failing to offer you some factor, some quantity, some formula, that will indicate it is mathematically more difficult to sit up from head down. Something one might vaguely expect perhaps from some vague idea of gravitational effects above or below the horizontal line... Or that's how my vague head vaguely thought of it all...

But maybe that's because there is no such factor, quantity, formula and it is, in mathematics and physics, simply no harder.

The 'more hard' is subjective to the human body and its musculature and to the basic difference in the two tasks - one, in fact, being a greater task than the other as stipulated in the beginning.

 

[oreo]

I think it depends on how you stand up straight from bed. I am considering one usual case. Suppose you are lying on bed. First you would sit up. That will require Torque acting at your pivot point i.e hip bone. Then you will apply torque on your knee joint equal to mg*r. Where m is mass of your body above knee joint and r is length of your bone from hip to knee.

 

[oreo]

I think you will require 2 torques. First to make you sit from liying position in which your hip bone is pivot. Then to stand, knee joint as pivot. I hope that's helpful

 

[A.T.]

I thought this might be helpful, a database with measured internal loads in the spine:

http://www.orthoload.com/database/

As "implant" choose "Vertebral body replacement" or "Internal spinal fixation". As activity "from lying to sitting".

 

[CWatters]

.. intuition tells me it can't just be that, because if the bed were flat, sitting up the torso from a flat 0 degrees to 90 and then 20 degrees more towards the feet, is not as hard.

Your intuition is wrong. These two situations are not the same.

In the first the "extra" 20 degrees is from -20 to 0 (horizontal). The centre of mass of the torso is being raised so you are doing work against gravity.

In the second the "extra" 20 degrees is from 90 (vertical) to 110. The centre of mass of the torso ends up lower as you bend forward so you are doing no work against gravity. (aside: It still takes some effort because you have to compress your stomach etc.)

It's not just the extra angle that matters. It's where that extra angle occurs.

One problem with analysing situations involving the human body is that the human body is inefficient. For example...Suppose you do a partial sit up to the 45 degree position and hold in that position. After awhile it will get harder and harder to remain in that position until your stomach will be screaming at you to stop. It feels like you are doing lots of work but you aren't. On the way up to 45 degrees you are doing work against gravity. Once you reach the 45 degree position and stop you are no longer raising your centre of mass so you are doing no work against gravity. The pain you feel while holding in that position is entirely due to the inefficiency of the human body.

 

[CWatters]

Ok here is my last attempt to explain it in terms of the work done against gravity..

 

[marciokoko]

Thanks CWatters. So you would say that in the first scenario you make 90 degrees against gravity but in the second you make in 110 degrees against gravity?

 

[sophiecentaur]

In addition to CW's mechanical explanation (which is, of course, sufficient), there is the psychological factor. As you raise your body from horizontal, the required force / torque gets less from the start. (Cos(θ) drops from 1 towards zero). When pulling up from below the horizontal, the required force actually increases as you approach horizontal. That can make the process appear to take more effort.
The Forces and the Energy involved in this process are all relevant to how 'hard' the action feels. It is easy to mix the two up. Also, the angles and heights involved are governed by trigonometry - adding possible confusion. Thus, moving from -45° to +45° involves a different change of height than from 0° to 90° and hence a different amount of Work needed.

 

[CWatters]

Thanks CWatters. So you would say that in the first scenario you make 90 degrees against gravity but in the second you make in 110 degrees against gravity?

Looks like I am confusing you.

There are two ways to calculate the work done...

1) Work = force * displacement

In this case "displacement" is the vertical displacement of the centre of mass. It's different for the 90 and 110 cases due to basic geometry. Force is the weight of the upper torso which is a constant depending on your mass.

2) Work = torque * angular displacement

In this case "angular displacement" is (the radian equivalent of) 90 or 110 degrees. The problem is that Torque is not constant, it's also dependent on the weight of the upper torso but it also varies with the angle making the maths harder.

The two methods give the same answer but 1) is probably easier to understand and calculate.

With the above you can calculate the work done against gravity and that should account for most of the difference between 110 and 90 degrees.

It's interesting to note that if you do a sit up and then lay back down the net displacement is zero as your torso is back where it started. So the net work done is zero. However it sure doesn't feel like you have done no work. What happened is that you do work against gravity on the way up and gravity does work on you on the way back down. It's just hard luck that humans have no way to collect and store the energy that gravity does on you. It ends up being wasted.

 

[marciokoko]

Im sure pretty soon we will when IoT continues invading the health industry.

Anyway, back to my question. Let's say I don't want to calculate anything.

Is there a way to answer the question:

"Why does it feel harder to do a situp from -20 to 90 then from 0 to 90?". Is it really harder? Is it just the fact that more work is being done?

It may seem unbelievable that after 55 posts I am still not clear, but I have gotten sidetracked by some other comments.