How to calculate the HP/torque required to rotate a dual sprocket/chain system?

[ScottyP99]

Hi,

I am trying to determine the HP motor/torque that will be required to rotate the sprocket/chain system in the image below from a resting position.

The sprockets will be at rest, rotate 5 degrees, come to a stop for 5 minutes, and then rotate again 5 degrees, repeated.

The speed of rotation is not important, but must be slow.

The motor will be attached to the top sprocket.

Thank you in advance for your help !

 

[berkeman]

Wow, that's a heavy chain and sprocket system! What is it turning? With such a heavy drive system, I'm guessing it is turning something else that is very massive.

Are you thinking of using a geared-down electric motor for this? Is the direction of rotation always the same, or does the system need to be able to change the direction of rotation?

Also, is this related to your "Gravity Battery" thread from last December?

https://www.physicsforums.com/threads/gravity-battery-systems.1009901/

 

[ScottyP99]

It will be turning pots full of liquid, equally distributed around the chain.

And the sprockets may be lighter, I am using that as a safe base.

Do not know much about motors yet, so wanted to figure out the power needed first.

Rotation direction is always the same, and the weight is equally distributed around the chain.

 

[berkeman]

So it sounds like you can model this as a simple turntable with weights distrubed around the circumference. The torque required will depend on the bearing friction of the system and the Moment of Inertia (MoI) of the system and the acceleration that is needed:
$$\tau = I \alpha + \tau_{friction}$$
The power (horsepower) required from the drive motor will depend on the gearing that you use between the motor and the driven system.

So let's start with your 2' radius drive gear, and assume some slow acceleration number. What is the total weight that will be moved by this system?

 

[berkeman]

Oh, and is this system horizontal or vertical? That will likely affect the bearing friction term. If vertical, are you lifting filled buckets of fluid and dropping emptied buckets? (and you didn't answer my question about the Gravity Battery thread...)

 

[russ_watters]

I am trying to determine the HP motor/torque that will be required to rotate the sprocket/chain system in the image below from a resting position.

The sprockets will be at rest, rotate 5 degrees, come to a stop for 5 minutes, and then rotate again 5 degrees, repeated.

The speed of rotation is not important, but must be slow.

The speed (or rather the acceleration) really is important to the calculation. For the system you have described, there is zero steady-state load except for friction (and a chain does have complicated friction). This means that despite the weight, the power requirement is really low. By comparison my telescope mount slings 100 lb at 3 degrees per second using about 1/20th horsepower.

 

[ScottyP99]

The total weight of the chain will be 700 lbs.

And the system is vertical. And no it will be rotating full buckets (it will load them one at a time so initially the weight will be small, and then once loaded it will rotate for 30 days as described below.

And sorry about the gravity battery question I missed, let me look back thru and see and I will answer.

Thank you !

 

[ScottyP99]

The speed (or rather the acceleration) really is important to the calculation. For the system you have described, there is zero steady-state load except for friction (and a chain does have complicated friction). This means that despite the weight, the power requirement is really low. By comparison my telescope mount slings 100 lb at 3 degrees per second using about 1/20th horsepower.

Thanks Russ. The system only rotates 5 degrees, so the speed has to be very slow, but has no real required value.

 

[berkeman]

it will load them one at a time so initially the weight will be small

How heavy are the buckets filled with liquid? The highest torque requrement will be to lift the first half of the buckets (the load on the system will be unbalanced by the weight of half of the filled buckets).

 

[ScottyP99]

Thanks Russ. The system only rotates 5 degrees, so the speed has to be very slow, but has no real required value.

Could we use a calculation that we have 5 degrees rotation in 15 seconds ?

So a 2' diameter sprocket wound have perimeter = 2 * 3.14 * 1 = 6.28 ft

5/360 = .0139 rotations => .0139 * 6.28 = .087 ft = 1.044" traveled in 15 seconds => 0.0058 ft/sec ??

 

[ScottyP99]

How heavy are the buckets filled with liquid? The highest torque requrement will be to lift the first half of the buckets (the load on the system will be unbalanced by the weight of half of the filled buckets).

There will be 40 buckets total @ 17.5 lbs ea. The buckets will be loaded from the side near the top (@ 8') one at a time, so the lift (up) side will only have 2-3 buckets before they rotate over the top and provide gravity pull on the down side. So I would think that power required would similar or less than the power to start and turn a fully loaded system.

And sorry I misunderstood your question, no this is not related to the gravity battery questions you helped me with previously.

Thanks

 

[russ_watters]

There will be 40 buckets total @ 17.5 lbs ea. The buckets will be loaded from the side near the top (@ 8') one at a time, so the lift (up) side will only have 2-3 buckets before they rotate over the top and provide gravity pull on the down side. So I would think that power required would similar or less than the power to start and turn a fully loaded system.

It's very different if the load is not balanced. The torque required is much higher, but fortunately since the rotation rate is very slow you can still generate a high torque with a small motor and gearing.

 

[berkeman]

The buckets will be loaded from the side near the top (@ 8') one at a time, so the lift (up) side will only have 2-3 buckets before they rotate over the top and provide gravity pull on the down side.

So you initially said that you only needed torque in one direction, but now it sounds like you need reverse torque until the first buckets get to the bottom, no?

 

[ScottyP99]

So you initially said that you only needed torque in one direction, but now it sounds like you need reverse torque until the first buckets get to the bottom, no?

No this will only rotate in one direction.

 

[ScottyP99]

Once all buckets are added the system will rotate multiple (1000s) times fully loaded.

 

[berkeman]

No this will only rotate in one direction.

Doesn't matter. When you get 1/2 of the buckets loaded, that will pull the chain down on that side. It will take a counter-torque to maintain a constant chain speed until you get to about 3/4 of the buckets loaded. You see that, right?

 

[ScottyP99]

Doesn't matter. When you get 1/2 of the buckets loaded, that will pull the chain down on that side. It will take a counter-torque to maintain a constant chain speed until you get to about 3/4 of the buckets loaded. You see that, right?

Understood. It will only rotate a couple inches each turn, and rotate 1000s of times after loading, so I am not really concerned about a constant rotation speed while loading.

Could you help me with the calcs for when its fully loaded and then I can look into the loading and unloading scenarios ?

 

[berkeman]

Understood. It will only rotate a couple inches each turn, and rotate 1000s of times after loading, so I am not really concerned about a constant rotation speed while loading.

Okay, but I think we need to consider the back-torque situation in this design. If you have an electric motor with a large ratio gearbox interface, I'm not sure how it will react when subjected to back-torque like this. Hopefully it doesn't lock up, but I would need more experienced opinions from the likes of @jrmichler and @Baluncore

 

[ScottyP99]

Okay, but I think we need to consider the back-torque situation in this design. If you have an electric motor with a large ratio gearbox interface, I'm not sure how it will react when subjected to back-torque like this. Hopefully it doesn't lock up, but I would need more experienced opinions from the likes of @jrmichler and @Baluncore

Definitely would love their input as well !

 

[jrmichler]

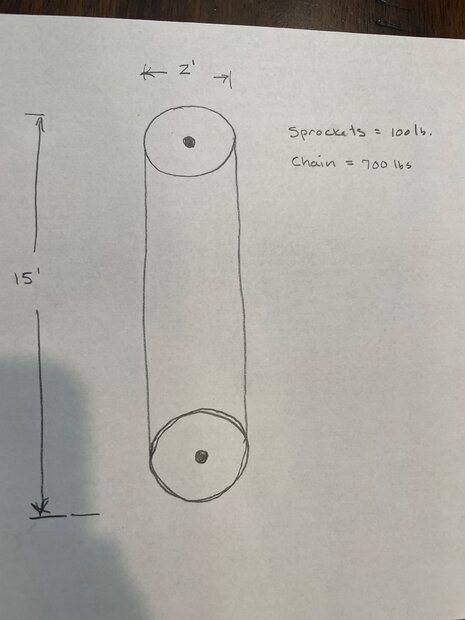
An engineering design problem such as this is done in a series of steps, generally with some iteration in the process. The following is one possible approach:

1) Calculate the maximum load on the top sprocket. Weight of chain, all buckets full, plus estimated chain pretension.

2) Calculate maximum torque on the drive sprocket. Assume that all buckets on one side of the centerline are full, and all buckets on the other side are empty. This is a worst case calculation, not a realistic case calculation. Then add in estimated friction for the nondrive sprocket, plus chain friction. If in doubt, add 50% or so.

3) Calculate RPM. You stated 5 degrees per 15 seconds, so 20 degrees per minute, which equals 0.055 RPM.

4) Calculate a gear ratio. A standard induction motor runs 1800 RPM, the load runs 0.055 RPM, so the initial try gear ratio is 1800 / 0.055 = 32,400:1.

5) You can get a clean design by mounting the drive sprocket directly on the output shaft of the gear reducer. The gear reducer output shaft must have a design radial load rating greater than the maximum load from Step #1. The reducer output shaft torque rating must be greater than the torque from Step #2.

6) Start looking at gear reducer catalogs. Some names to start with include Boston Gear, Rexnord, Alpha, Stober, and Falk. These names are off the top of my head, there are other just as good. You will quickly find standard designs with gear ratios up to 3600:1. You can use a 3600:1 gear reducer if you run the motor through a Variable Frequency Drive (VFD), and run the motor at 11% speed. This step will take a few hours, or more likely, days because industrial gear reducers are available in a huge number of configurations. The gear reducer catalog will have information on drive torque and power at the rated output torque. Those numbers take into account the reducer friction, which can be significant in a high ratio reducer.

7) Now you can choose a drive motor and VFD for that motor. A simple low speed system such as this can be driven by a standard induction motor. No need for acceleration calculations, just turn the motor on and off to operate it.

8) The reducer will almost certainly be a double reduction worm gear. It will be self locking, so turning off the motor will stop it from moving. Cutaway view of a double reduction helical / worm gear reducer is shown below. The motor is fastened to the flange on the upper right, the output shaft is lower left in front:

 

[Baluncore]

Definitely would love their input as well !

You asked for it.

The tension, quality and lubrication of the chain will be critical to deciding the torque needed to advance the mechanism. Each time the chain is advanced it will need to be bent onto the sprockets, and then pulled straight again as it disengages from the sprockets. Chain lubrication will attract dirt which will cause wear and friction.

A big sprocket will require the stretching chain be replaced more often as tooth pitch is critical on big sprockets.
With the chain system, the two sprockets should be replaced with 2 foot diameter plain wheels without spurs. Then, rather than turning the shaft of the 2 foot diameter sprocket, the smallest diameter sprocket (11 tooth?) can then be used to advance the chain with a factor of about 10 in gear ratio advantage. The small sprocket can be replaced more easily and cheaply as the one chain wears and so stretches over the much longer life of the machine.

So now I wonder why you use a 36.28 foot chain when a single 15 foot diameter wheel would solve much of the exposed lubrication problem. Indeed, for the same circumference as the length of chain, the wheel could be reduced in diameter to about 11.5 foot.

The upper sprocket bearing will need to carry the entire weight of the chain system. With a single wheel, that same bearing would carry the weight of the wheel and could be a fully sealed, lubricated roller bearing. Keep it clean by avoiding the exposed chain.

Wheel drive could be through the circumference rather than the shaft. That would reduce the motor gearing required.

With a wheel, the buckets could be housed within the wheel periphery. Maybe two layers of buckets could be used, reducing the wheel diameter required to between 6 and 8 foot.