How to calculate the kinetic energy of an object propelled by a magnet?

[pete94857]

TL;DR Summary

How to calculate the kinetic energy of an object propelled by a magnetic field.

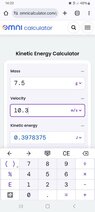
How to calculate the kinetic energy of an object propelled by a magnetic field. For example I have 2 magnets face to face in opposition. Each magnet is a N42 Neodymium cube dimensions 10, 10, 10 mm they are in free space with no interference. The maximum pull strength is 4.7 kg. If I were to release one magnet allow it to move away freely to 100 mm where it collides to collect its kinetic energy with a maximum collection efficiency. How much kinetic energy would there be.

 

[anuttarasammyak]

If during 100 mm move force on magnet is kept 4.7 kgw, the work done so kinetic energy of magnet acquired is
4.7 x 0.98 Newton ｘ　0.1 m = 0.46 Jule

 

[kuruman]

A magnet shaped like a cube is unlikely to generate a constant repulsive force over a distance that is 10 times the side of the cube. Nevertheless the idea of using the work-energy theorem is a good way to proceed. One can obtain a more realistic estimate of the kinetic energy by considering both cubes as magnetic dipoles each with dipole moment $\mathbf m.$ The dipoles are initially antiparallel along the z-axis at initial separation $z_0$. One of them is fixed on the axis whole the other is free to move along the axis. The force on the free dipole is $$\mathbf F=(\mathbf m\cdot \mathbf {\nabla})\mathbf B$$ where $\mathbf B$ is the dipolar field of the fixed dipole, $\mathbf B \sim \dfrac{\text{const.}}{z^3} .$ With all vectors along the z-axis, we can write the force $$\mathbf F=-F_0\frac{z_0^4}{z^4}$$where $F_0$, e.g. $4.7\times 9.8~$N, is the value of the force when the magnets are separated by distance $z_0$ which is assumed known. If the magnet is released at that separation, its change in kinetic energy after distance $z$ from the magnet will be $$\Delta K =-F_0 z_0^4 \int_{z_0}^z \frac{dz}{z^4}.$$This is just an estimate in the approximation that the cubes behave as point dipoles.

 

[pete94857]

The main points that is confusing me are.

1. your calculations you seem to assume the force remains constant over the distance ? For example the force rapidly drops off over the distance. Although a force is still applied but less than the original.

2. How to think of the force as it drops off, even though the force reduces does the still applied force accumulate because the actual speedof the feild although reduces in strength remains the same speed ? Or thinking of a magnetic like a holding force does the reduced strength actually take away from the original force by causing a slowing as the strength of the field reduces ?

 

[anuttarasammyak]

1. your calculations you seem to assume the force remains constant over the distance ? For example the force rapidly drops off over the distance. Although a force is still applied but less than the original.

In general work done so kinetic energy gained is
$$\int F(x) dx$$
We need F(x) force as a function of position to calculate this integral.

 

[pete94857]

If during 100 mm move force on magnet is kept 4.7 kgw, the work done so kinetic energy of magnet acquired is
4.7 x 0.98 Newton ｘ　0.1 m = 0.46 Jule

4.7 x 0.98 , why 0.98 ? If I convert 4.7 khf to Newtons its 46.091255 Newtons then x 0.1 m for work done, ( obviously disregarding how the feild strength changes over the distance) = 4.609 joules

 

[pete94857]

4.7 x 0.98 , why 0.98 ? If I convert 4.7 khf to Newtons its 46.091255 Newtons then x 0.1 m for work done, ( obviously disregarding how the feild strength changes over the distance) = 4.609 joules

Sorry typo 4.7 kgf

 

[pete94857]

In general work done so kinetic energy gained is
$$\int F(x) dx$$
We need F(x) force as a function of position to calculate this integral.

Unless you are converting to Nm but then you are x by distance again at 0.1 , it seems to make more sense to me 4.7 x 0.98 Nm = J

 

[pete94857]

A magnet shaped like a cube is unlikely to generate a constant repulsive force over a distance that is 10 times the side of the cube. Nevertheless the idea of using the work-energy theorem is a good way to proceed. One can obtain a more realistic estimate of the kinetic energy by considering both cubes as magnetic dipoles each with dipole moment $\mathbf m.$ The dipoles are initially antiparallel along the z-axis at initial separation $z_0$. One of them is fixed on the axis whole the other is free to move along the axis. The force on the free dipole is $$\mathbf F=(\mathbf m\cdot \mathbf {\nabla})\mathbf B$$ where $\mathbf B$ is the dipolar field of the fixed dipole, $\mathbf B \sim \dfrac{\text{const.}}{z^3} .$ With all vectors along the z-axis, we can write the force $$\mathbf F=-F_0\frac{z_0^4}{z^4}$$where $F_0$, e.g. $4.7\times 9.8~$N, is the value of the force when the magnets are separated by distance $z_0$ which is assumed known. If the magnet is released at that separation, its change in kinetic energy after distance $z$ from the magnet will be $$\Delta K =-F_0 z_0^4 \int_{z_0}^z \frac{dz}{z^4}.$$This is just an estimate in the approximation that the cubes behave as point dipoles.

Sorry I'd need more detailed explanation to understand your answer. An explanation to every point of each formula. I understand your concept.

 

[anuttarasammyak]

4.7 x 0.98 , why 0.98 ? If I convert 4.7 khf to Newtons its 46.091255 Newtons then x 0.1 m for work done, ( obviously disregarding how the feild strength changes over the distance) = 4.609 joules

You are right. 9.8, not 0.98.

 

[pete94857]

You are right. 9.8, not 0.98.

I see. Thanks. But how should we think of the force provided by the rest of the field ? The 4.7 kgf is only for a very short amount of time then the field strength diminishes quickly. But I thought energy goes in it stays in unless something acts against it. So would the energy accumulate ? But in practical experiment it doesn't seem to accumulate although I could be wrong. Or does the lesser strength actually take energy away acting like a holding force. I'm very unsure.

 

[pete94857]

Maybe regarding the changing force finding the average over the distance assuming the force is applied over the full distance then multiply by distance. 4.7 start 0 end average of 2.35 x 9.8 x 0.1 = 2.303 Joules

 

[pete94857]

I broke it down to 1 mm distances. Over 66 mm at which point the feild strength was insignificant. I then performed a work calculation per 1 mm to gain the joules, I got the feild strength from a online field strength calculator. I then added up the joules from each 1mm and it came to 0.3673 j per magnet. I then found out the 2 magnets working together is no a simple doubling but rather the percentage increase changes over distance so I used an average of plus 70%. So the answer to my question is approximately 0.62441 J.

 

[pete94857]

I broke it down to 1 mm distances. Over 66 mm at which point the feild strength was insignificant. I then performed a work calculation per 1 mm to gain the joules, I got the feild strength from a online field strength calculator. I then added up the joules from each 1mm and it came to 0.3673 j per magnet. I then found out the 2 magnets working together is no a simple doubling but rather the percentage increase changes over distance so I used an average of plus 70%. So the answer to my question is approximately 0.62441 J.

And have a velocity of approximately 10 m/s2 taking approximately 0.66 seconds to complete the movement.

 

[kuruman]

I broke it down to 1 mm distances. Over 66 mm at which point the feild strength was insignificant. I then performed a work calculation per 1 mm to gain the joules, I got the feild strength from a online field strength calculator. I then added up the joules from each 1mm and it came to 0.3673 j per magnet. I then found out the 2 magnets working together is no a simple doubling but rather the percentage increase changes over distance so I used an average of plus 70%. So the answer to my question is approximately 0.62441 J.

If you are posting these numbers expecting confirmation that they are correct, you need to provide more detailed information.
1. You say you used an online field strength calculator. Where did you find it? More importantly what was the input to the calculator and how did you use its output to find work per 1 mm?

2. You say "I then found out the 2 magnets working together is no a simple doubling but rather the percentage increase changes over distance so I used an average of plus 70%." What on Earth is that all about? What, specifically did you find out that made you draw this conclusion? It seems that you are calculating the work done on each magnet and then claim that adding the two works (a simple doubling) is not the same as "the two magnets working together". How did you do this second calculation? Energy is conserved, so if your additional calculation says that 30% of the 2×0.62441 Joules is lost you must explain where it went.

And have a velocity of approximately 10 m/s2 taking approximately 0.66 seconds to complete the movement.

3. How did you find the numbers for velocity and time? What assumptions did you make? Also, m/s2 is not the appropriate units for velocity which are m/s. If you meant m/s², these are units of acceleration. So which did you calculate, velocity or acceleration?

 

[pete94857]

If you are posting these numbers expecting confirmation that they are correct, you need to provide more detailed information.
1. You say you used an online field strength calculator. Where did you find it? More importantly what was the input to the calculator and how did you use its output to find work per 1 mm?

2. You say "I then found out the 2 magnets working together is no a simple doubling but rather the percentage increase changes over distance so I used an average of plus 70%." What on Earth is that all about? What, specifically did you find out that made you draw this conclusion? It seems that you are calculating the work done on each magnet and then claim that adding the two works (a simple doubling) is not the same as "the two magnets working together". How did you do this second calculation? Energy is conserved, so if your additional calculation says that 30% of the 2×0.62441 Joules is lost you must explain where it went.

3. How did you find the numbers for velocity and time? What assumptions did you make? Also, m/s2 is not the appropriate units for velocity which are m/s. If you meant m/s², these are units of acceleration. So which did you calculate, velocity or acceleration?

A lot of questions...

On line feild calculator https://www.kjmagnetics.com/calculator.repel.asp?calcType=block

Online physics calculator https://www.omnicalculator.com/physics/kinetic-energy ... yes you're correct m/s not m/s2 my mistake. See attached for velocity calculation.


I've tried to find the physics website that told me about the percentage with reference the moving magnet but I can't find it, I closed the tab after. But the feild strength will double but the actual force acting on the moving magnet varies with distance and configuration therefore it not a doubling of force acting on the moving magnet.

Was I knew the velocity because I had the work I could the determine the amount of time it would take to travel the given distance.