Leopold89
- 59
- 5
Dear forum,
I was trying out two different approaches to calculate the dimensions of a ring resonator (sketch below) and got two slightly different solutions.
The first approach is to assume that the waveguide wavelength has to fit n times onto the circumference of the ring (taking the average of outer and inner radius): $$2\pi r = n \lambda_{waveguide}$$, with the longer waveguide wavelength. This works well.
The second approach is to solve the Laplace equation in cylindrical coordinates, yielding the condition $$J_m(\alpha r_{in})Y_m(\alpha r_{out})=J_m(\alpha r_{out})Y_m(\alpha r_{in})$$ for the radii, with $$\alpha=\frac{2\pi}{\lambda}$$ as wave number.
I noticed that the solutions to the second condition are more of less slightly off, so I wanted to ask why the second approach does not work.
My guess is that I need to take the surface charges at the end of the waveguide into account. But what I don't understand is that I would want to have the waveguide as long as half a waveguide wavelength, so wouldn't I get no field and therefore no charge at the intersection of waveguide and ring?
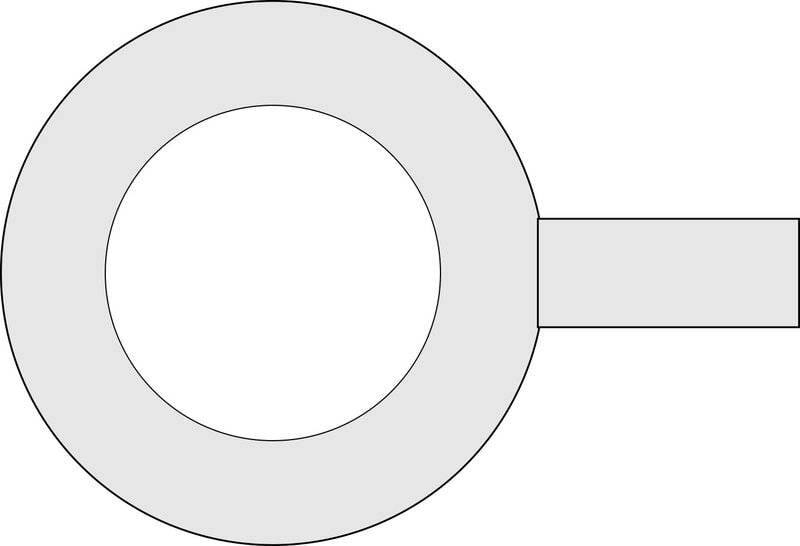
I was trying out two different approaches to calculate the dimensions of a ring resonator (sketch below) and got two slightly different solutions.
The first approach is to assume that the waveguide wavelength has to fit n times onto the circumference of the ring (taking the average of outer and inner radius): $$2\pi r = n \lambda_{waveguide}$$, with the longer waveguide wavelength. This works well.
The second approach is to solve the Laplace equation in cylindrical coordinates, yielding the condition $$J_m(\alpha r_{in})Y_m(\alpha r_{out})=J_m(\alpha r_{out})Y_m(\alpha r_{in})$$ for the radii, with $$\alpha=\frac{2\pi}{\lambda}$$ as wave number.
I noticed that the solutions to the second condition are more of less slightly off, so I wanted to ask why the second approach does not work.
My guess is that I need to take the surface charges at the end of the waveguide into account. But what I don't understand is that I would want to have the waveguide as long as half a waveguide wavelength, so wouldn't I get no field and therefore no charge at the intersection of waveguide and ring?