How to Calculate Thevenin Equivalent Circuit

[LearnerErnie]

Homework Statement

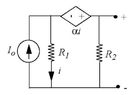
Find the Thevenin equivalent circuit of the attached circuit. Assume that α has units of Ohms.

Relevant Equations

KCL: The sum of currents into and out of a node in a circuit equals 0.
KVL: The sum of voltages in any closed loop is 0.
V = IR

First, I calculate the Thevenin resistance by treating the independent current source I₀ as an open circuit and noticing that the resistance of the dependent voltage source is α (since V=IR and the voltage across the dependent voltage source is given by αi.

In this way, I have:

R_TH = 1 / (1 / R₂ + 1 / (R₁ + α)) = (R₁ + α)R₂ / (R₁ + R₂ + α)

Now, for the Thevenin voltage V_TH, I thought it might be easier to find the short circuit current I_N through the output terminals and then simply multiply by R_TH to get V_TH.

This is where my analysis gets confused.

I've attached my redrawn circuit when I short the output terminals. Using this circuit, I think I can say the following using KCL:

I₀ = I₁ + I₁ (since the current through the CCVC is I₁)

I₁ = I₂ + I_N (can I ignore I₂ since the current will completely avoid the resistor and prefer the shorted path?)

If I can ignore the resistor, then I₁ = 0 + I_N.

At this point, I get a bit stuck. The equations don't really seem to tell me anything useful, and I don't think that I_N = I₁, but I don't know where my confusion lies exactly.

If I write out all the branch currents explicitly and solve it in a very granular fashion, I find that I_TH = I₀, but I do not know how to derive this result in a more "intuitive" manner.

If someone could point me in the right direction, that would be very helpful. Thanks.

 

[lewando]

...the resistance of the dependent voltage source is α (since V=IR and the voltage across the dependent voltage source is given by αi.

α is just a scale factor for determining the voltage of the CCVS. It happens to have units of ohms, but it is not the internal resistance of the CCVS. A dependent source is like an independent source--it has no internal resistance.

 

[LearnerErnie]

α is just a scale factor for determining the voltage of the CCVS. It happens to have units of ohms, but it is not the internal resistance of the CCVS. A dependent source is like an independent source--it has no internal resistance.

Ah got it! Thanks very much! So we've effectively shorted the entire circuit, since the current will take the path of least resistance, meaning $I_N = I_0$? I think this means the current through the CCVC must be $I_0$? If so, that's super intuitive and makes perfect sense. If not...I guess I'm even more confused ...

That also means that $R_{TH}$ was calculated incorrectly. So we have

$$R_{TH} = \frac{R_1R_2}{R_1 + R_2} \quad\text{and}\quad I_N = I_0$$

Thus, $$V_{TH} = \frac{I_0R_1R_2}{R_1 + R_2}$$

I still feel like I'm missing something, since I haven't used the CCVC at all.

 

[DaveE]

I still feel like I'm missing something

Does it make sense to you that α doesn't appear anywhere in your solution? What if Io, R1, and R2 were all set to 1 and α varied from 0 → ∞. Would you expect the circuit to behave differently?

One way to find the Thevenin equivalent is to use the calculations for the open circuit voltage and the short circuit current. Try again with that approach.

 

[lewando]

I could have been clearer, so my apologies. I did not mean zero resistance. I should have said these are ideal active devices and cannot be modeled a resistor. It is true that for a given DC operating point there will be a voltage across and current through a dependent source leading you to think about a resistance. But under different load conditions, or different circuit component values, the dependent source will try to maintain its constant voltage (or current) and yet allow the corresponding current (or voltage) to change as needed.

 

[DaveE]

Yes.
A voltage source (dependent, or not) WILL have the defined voltage across it with whatever current through it that the circuit generates as a consequence of its, and other, voltages. Voltage sources have, by definition, 0Ω of series resistance, since the voltage will not change as a function of the current through it. Current sources are similar; their current is defined and it won't change if the voltage across it changes. They have infinite series resistance (or 0 shunt resistance for the Norton equivalent). Their voltage is entirely dependent on how the rest of the circuit responds to the current that MUST be flowing through the current source.