How to change the frequency values inside a time domain signal phase

[tworitdash]

The problem I am having is simple. I have a Gaussian spectrum initially. Like this,

Process 1:

S = m0/sqrt(2*pi*sigma^2) * exp(-(vel_axis - mu).^2/(2*sigma^2));

Here, mu is the mean velocity (frequency) and sigma is the standard deviation. vel_axis is the axis on which I am calculating this Gaussian spectrum.

Then, with the help of random phase generators and using an inverse Fourier transform, I calculate the time domain signal of this spectrum.

s = ifft(fftshift(sqrt(N) .* sqrt(S) .* exp(1j .* Theta))); %timedomain

Here Theta is the uniform random phase between -pi to pi and N is the number of sampling points.

Process 2:

Now, I want to change the phase of the signal in the time domain to see the changes again in frequency domain.

s_modified_in_time_domain = abs(s) .* exp(1j .* unwrap(angle(sig)) .* (-1))

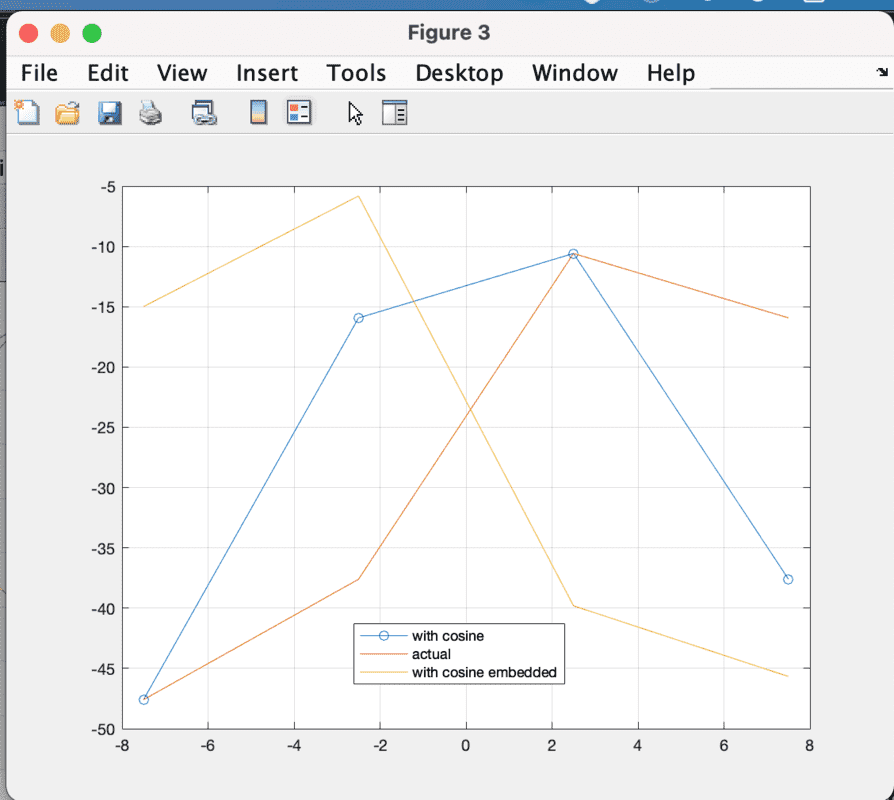
Here, I have multiplied (-1) so that I will have a spectrum around the value of -mu instead of mu. That is the idea. However, the spectrum is not around -mu and it is shifted to the positive axis of velocity (frequency). I have attached a plot to this post where it can be seen by the blue signal. The red signal is the actual time-domain signal of Process 1 in the frequency domain. And the Gaussian is around mu. Here mu is 5 [m/s].

Process 3:

Instead of doing the modification in the time domain, if I modify it in process 1 and in the equation of S, if I use -mu, instead of mu I get the desired result.

Therefore, I don't know why I get a shift in the plot of Process 2. Any idea if the equation for lower case s (equation number 2) does something weird?

In the plot: Blue is process 2 in the frequency domain Red is Process 1 with mu = 5 Yellow is Process 1 with mu = -5

The Blue plot should resemble the Yellow plot but it shifted towards the right. I want to do the change in the time domain and see the effect in the frequency domain. How can I use Process 2 in a good way. Just to show this effect I have used N as 4. So, it is very poorly sampled.

The code is done in MATLAB. This is just the idea. the code is lengthy with other things.

 

[mmwave]

Thank you for sharing your problem with us. After reviewing your processes and equations, I believe I have found the issue with Process 2.

In Process 2, when you are modifying the phase of the signal in the time domain, you are using the angle of the original signal (sig) instead of the modified signal (s). This means that the phase shift is not being applied correctly and is causing the spectrum to shift to the positive axis of velocity.

To fix this, you should use the angle of the modified signal (s) in the equation. This will ensure that the phase shift is applied correctly and the spectrum will be centered around -mu as desired.

I hope this helps and please let me know if you have any further questions or concerns.
Scientist