Vigardo
- 87
- 7
- TL;DR Summary
- I´m need a method to determine 2D or 3D truss stability without solving complex matrix equations. It should be easily implemented in a computer program. Thanks!
Dear experts,
I´m searching for some method to determine whether any 2D or 3D truss is stable without solving complex matrix equations. I want to implement such method in a simple computer program to discard any a priori non-stable trusses for further analysis.
Do you know any book or reference where this may be well explained? Can you help me?
So far, I´ve found that the condition of stability can be expressed mathematically as M + R >= 2J for a 2D planar truss of M members, R support reactions, and J joints. Similarly, the condition becomes M + R >= 3J for a 3D space truss [1]. In case such conditions were not fulfilled, the truss should be Instable due to Partial Constraints.
However, fulfilling such conditions does not guarantee stability, it just seems to be something "necessary" but not "sufficient" to asses truss stability.
In [2], it is said that for planar trusses, the structure may yet be Unstable due to Improper Constraints when:
A) All of the reactive forces are parallel for the entire truss or any component part of the truss;
B) All of the reactive forces are collinear (intersect at one point) for the entire truss or any component part of the truss.
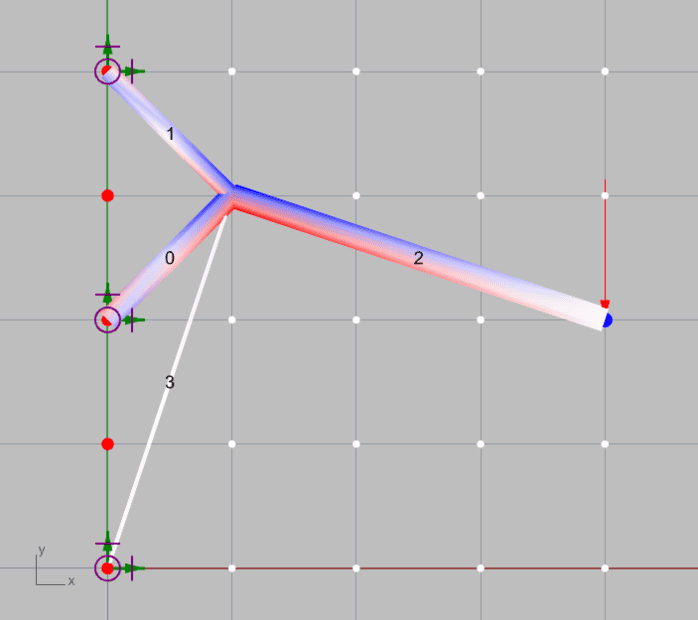
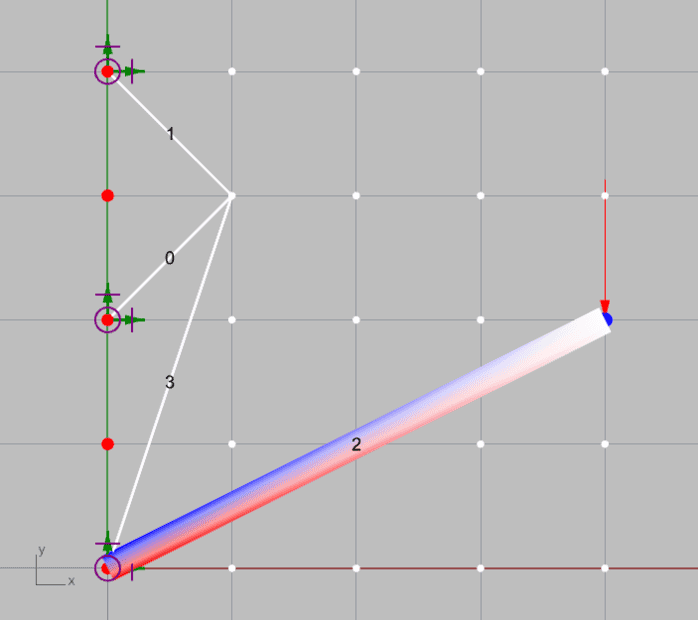
For example, the following structures fulfill such condition (M=4, R=6 and J=5, and thus M+R>=2J), but evidently they are not stable.
Please, don´t hesitate to correct me if I´m wrong at any point. Thanks!
I´m searching for some method to determine whether any 2D or 3D truss is stable without solving complex matrix equations. I want to implement such method in a simple computer program to discard any a priori non-stable trusses for further analysis.
Do you know any book or reference where this may be well explained? Can you help me?
So far, I´ve found that the condition of stability can be expressed mathematically as M + R >= 2J for a 2D planar truss of M members, R support reactions, and J joints. Similarly, the condition becomes M + R >= 3J for a 3D space truss [1]. In case such conditions were not fulfilled, the truss should be Instable due to Partial Constraints.
However, fulfilling such conditions does not guarantee stability, it just seems to be something "necessary" but not "sufficient" to asses truss stability.
In [2], it is said that for planar trusses, the structure may yet be Unstable due to Improper Constraints when:
A) All of the reactive forces are parallel for the entire truss or any component part of the truss;
B) All of the reactive forces are collinear (intersect at one point) for the entire truss or any component part of the truss.
For example, the following structures fulfill such condition (M=4, R=6 and J=5, and thus M+R>=2J), but evidently they are not stable.
Please, don´t hesitate to correct me if I´m wrong at any point. Thanks!