- #1
Makonia
- 25
- 1
1. The prIoblem statement, all variables and given/known data
You are the chief of the Angry Birds (Google it, if you don’t know the reference...it’s not important). You can shoot red birds from a catapult, and they will fly as projectiles under the effect of gravity. Gravity points downwards and has magnitude g = 9.80 m/s2 . Your goal is to hit some nasty green pigs, who have stolen your Angry Bird Eggs. You are able to adjust the angle θ and speed v of the projectile, as it leaves the catapult. The projectile leaves the catapult at a height h above the ground.
a) First, consider the case when a single green pig is placed on the ground, at a distance d from the foot of the catapult. Find a relation between the angle and speed required to hit it. Remember to draw a sketch of the situation.
b) Next consider the case where there are two green pigs. One on the ground at a distance d as before, the other at a distance l < d, and placed on a pole of height h. What should you choose for θ and v in order to hit both pigs 1 with the same red bird? Why must one require l < d? Remember to draw a sketch of the situation.
On 1a) I came to the equation: Vi = sqrt((gd^2)/(2cos^(2)θ(h+d*tanθ)
I think i have to somehow use the equation from a in order to find the V initial and angle but I don't know how.
Because the distance between the two objects isn't given and the projectile can hit with either a small angle and large innitial speed or a large angle and low speed. The fact that I need to find an expression for both of these when the distance isn't given is what's troubbeling me and any hints or pointers to which direction I should go next would be much appreaciated :) (sorry for my bad english, but I hope you understand)
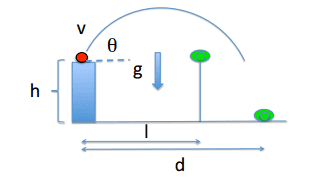
This is the drawing that came with it btw
The task is given to the chapter about projectile motion and i think I'm supposed to use projectile motion to solve it.
You are the chief of the Angry Birds (Google it, if you don’t know the reference...it’s not important). You can shoot red birds from a catapult, and they will fly as projectiles under the effect of gravity. Gravity points downwards and has magnitude g = 9.80 m/s2 . Your goal is to hit some nasty green pigs, who have stolen your Angry Bird Eggs. You are able to adjust the angle θ and speed v of the projectile, as it leaves the catapult. The projectile leaves the catapult at a height h above the ground.
a) First, consider the case when a single green pig is placed on the ground, at a distance d from the foot of the catapult. Find a relation between the angle and speed required to hit it. Remember to draw a sketch of the situation.
b) Next consider the case where there are two green pigs. One on the ground at a distance d as before, the other at a distance l < d, and placed on a pole of height h. What should you choose for θ and v in order to hit both pigs 1 with the same red bird? Why must one require l < d? Remember to draw a sketch of the situation.
Homework Equations
On 1a) I came to the equation: Vi = sqrt((gd^2)/(2cos^(2)θ(h+d*tanθ)
The Attempt at a Solution
I think i have to somehow use the equation from a in order to find the V initial and angle but I don't know how.
Because the distance between the two objects isn't given and the projectile can hit with either a small angle and large innitial speed or a large angle and low speed. The fact that I need to find an expression for both of these when the distance isn't given is what's troubbeling me and any hints or pointers to which direction I should go next would be much appreaciated :) (sorry for my bad english, but I hope you understand)
This is the drawing that came with it btw
The task is given to the chapter about projectile motion and i think I'm supposed to use projectile motion to solve it.
Last edited by a moderator: