How to construct 4 in+out Feynman diagram from 3 Feynman diagram?

[Martian2020]

TL;DR Summary

Sean Carroll stated 4 in/out lines Feynman diagram can be constructed from 3 lines one. What does it mean?

Renormalization talk by Sean Carroll, "but then I could construct from that the following diagram with four lines in it":

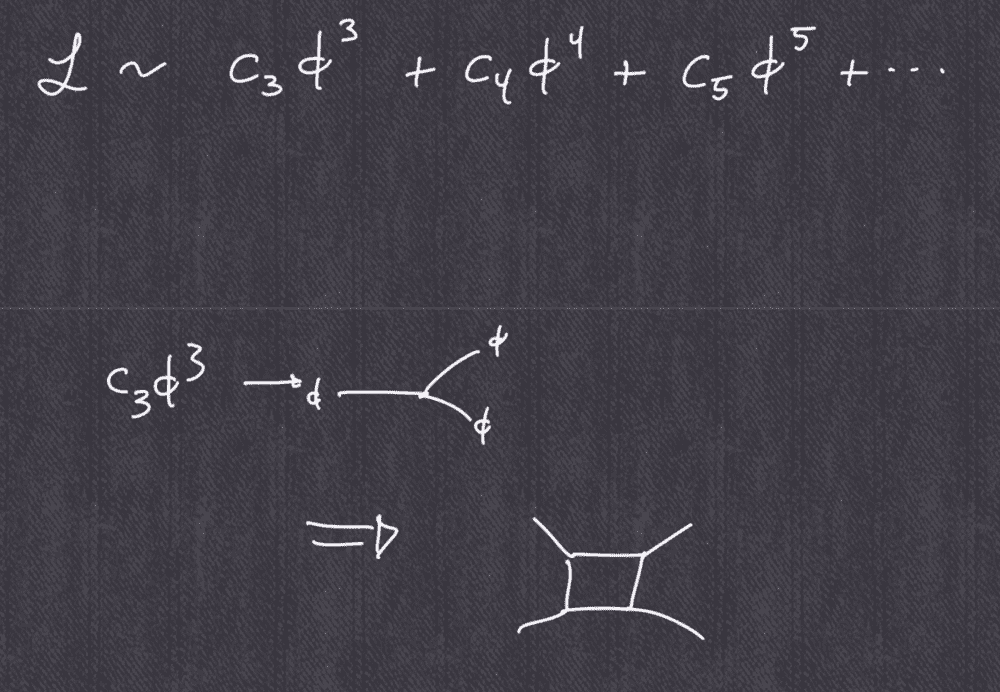
In previous talks he explained about diagrams and told interaction can be represented by many (even infinite) number of diagrams, "in" line can be changed to antiparticle "out" one, but for one particular interaction number of in+out lines was the same. In above he claims to construct 4 from 3. What does it mean? I was not able to find the answer by web search, google gives articles about diagrams "in general".

 

[vanhees71]

You can just draw any diagram consistent with the Feynman rules of the model under consideration. So you can draw the diagram shown in the picture. So even if you set all the constants $c_4=c_5=\ldots=0$ you can have vertices with an arbitrary number of lines.

In connection with renormalizability it's however important that you have all interactions in the Lagrangian such that the model is renormalizable. In this case you must thus keep $c_4$, because the drawn diagram is logarithmically divergent and you need a counter term to renormalize it, which means you must have a term like $c_4 \phi^4$ in the Lagrangian to make the model renormalizable.

On the other hand, you must not have $c_5 \phi^5$ and higher-order expressions, because then the theory wouldn't be (Dyson-)renormalizable anymore, but without such higher-order expressions the theory is indeed renormalizble, because the diagrams with $\geq 5$ legs are superficially convergent (and thus the entire theory given the BPHZ theorem of renormalization).

It's also interesting to look at electrodynamics with Dirac fermions (e.g., electrons and positrons). There you can also draw diagrams with four photon legs, and such a diagram is superficially logarithmically divergent, which would be a desaster, because then you'd have to find a gauge-invariant expression with four photon fields for your Lagrangian, and there's none that leads to renormalizable couplings. Fortunately gauge invariance saves the day, because the superficially divergent four-photon diagram is convergent thanks to a corresponding Ward-Takahashi identity.

 

[Haborix]

He just means that you can "glue" together vertices with three external lines together to make a diagram with four external lines.