How to decompose the following expression?

[Alec V]

This comes from one of the research papers that I'm reading. The authors decompose Eq. 1 and obtain Eq. 2. After several attempts, I have been fairly unsuccessful at obtaining Eq. 2 from Eq. 1.

I have tried using partial fractions decomposition without much success. Any help would be greatly appreciated.

Eq. 1

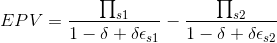
Eq. 2

Thanks!

 

[mfb]

Try to find the other direction, that is easier (and all steps work both ways). You can simplify equation 2 and get equation 1.

 

[Stephen Tashi]

Eq. 2

You have to explain the relations that exist among the symbols to get help on this question.

 

[Mark44]

Eq. 2

You have to explain the relations that exist among the symbols to get help on this question.

Yes, especially $\Pi_{s1}$ and $\Pi_{sS2}$. Are they just numbers or is something else going on? The symbol $\Pi$ is usually used to denote a product.

 

[Alec V]

Sorry, I should have clarified. ∏_s1 is profit in country 1, ∏_s2 is profit in country 2, ∈_s1 is risk in country 1, ∈_s2 is risk in country 2, and δ is the discount rate.

Eq. 2 tries to separate risk elements (∈_s1 and ∈_s2) from the profit gap between countries. Hope this helps.

 

[mfb]

∏ as variable is a bit unusual, but as long as all symbols are just variables, their meaning does not matter. This just needs the basic rules to work with fractions.

 

[Stephen Tashi]

The results of a simple numerical test did produce identical answers for EPV. (Of course someone should check my program.)

#include <stdio.h>
#include <math.h>void main()

{double pi_1, pi_2, delta, ep_1, ep_2;
double frac1,frac2, numerator, denom1, denom2;
double epv_1, epv_2;
pi_1 = 10.0;
pi_2 = 30.0;
delta = 0.25;
ep_1 = 6.0;
ep_2 = 5.0;
printf("pi_1 = %6.3f pi_2 = %6.3f delta = %6.3f ep_1 = %6.3f ep_2 = %6.3f\n\n",pi_1,pi_2,delta,ep_1,ep_2);

denom1 = 1.0 - delta + delta * ep_1;
frac1 = pi_1/denom1;
printf("frac1 %6.4f\n", frac1);
denom2 = 1.0 - delta + delta * ep_2;
frac2 = pi_2/denom2;
printf("frac2 %6.4f\n",frac2);
epv_1 = frac1 - frac2;
printf("epv_1 = %6.3f\n\n",epv_1);

frac1 = (pi_1 - pi_2)/ (1.0 - delta);
printf("frac1 %6.4f\n", frac1);
frac2 = ( delta * ( denom1 * ep_2 * pi_2 - denom2 * ep_1 * pi_1) )/ ((1.0 - delta)*denom1* denom2 );
printf("frac2 %6.4f\n",frac2);
epv_2 = frac1 + frac2;
printf("epv_2 = %6.3f\n", epv_2);}

The output

pi_1 = 10.000 pi_2 = 30.000 delta = 0.250 ep_1 = 6.000 ep_2 = 5.000

frac1 4.4444
frac2 15.0000
epv_1 = -10.556

frac1 -26.6667
frac2 16.1111
epv_2 = -10.556

 

[Stephen Tashi]

Getting rid of terms in a denominator that don't cancel with anything in the numerator is a frequent mathematical daydream. Suppose we approach the problem as the desire to express:

$( \frac{A}{W + F} - \frac{B}{W + G})$ as $( \frac{A}{W} - \frac{B}{W}) \ + \ L$

where $L$ is the leftover stuff.

Then
$L = \frac{A}{W+F} - \frac{A}{W} - \frac{B}{W + G} + \frac{B}{W }$

$= \frac{ AW - A(W+F)} {W(W+F)} + \frac{-BW+B(W+G)}{W(W+G)}$

$= \frac{-AF}{W(W+F)} + \frac{BG}{W(W+G)}$

$= \frac{1}{W} ( \frac{BG}{W+G} - \frac{AF}{W+F})$

In the problem at hand, there are relations between $W, F, G$

$W = 1 -\delta$
$F = \delta \epsilon_1 = (1-W)\epsilon_1$
$G = \delta \epsilon_2 = (1-W)\epsilon_2$

Substituting in selected places for $F$ and $G$

$L = \frac{1}{W}( \frac{B(1-W)\epsilon_2}{W+G} - \frac{A(1-W)\epsilon_1}{W+F} )$

$= \frac{1-W}{W} ( \frac{ \epsilon_2 B}{W+G} - \frac{\epsilon_1 A}{W+F})$

$= \frac{1-W}{W} ( \frac{ (W+F)\epsilon_2 B - (W+G)\epsilon_1A}{(W+G)(W+F)})$

In the problem at hand:
$A = \prod_{s1}$
$B = \prod_{s2}$
$W = (1 -\delta)$
$F = \delta \epsilon_{s1}$
$G = \delta \epsilon_{s2}$
$\epsilon_1 = \epsilon_{s1}$
$\epsilon_2 = \epsilon_{s2}$.

 

[Alec V]

Getting rid of terms in a denominator that don't cancel with anything in the numerator is a frequent mathematical daydream. Suppose we approach the problem as the desire to express:

$( \frac{A}{W + F} - \frac{B}{W + G})$ as $( \frac{A}{W} - \frac{B}{W}) \ + \ L$

where $L$ is the leftover stuff.

Then
$L = \frac{A}{W+F} - \frac{A}{W} - \frac{B}{W + G} + \frac{B}{W }$

$= \frac{ AW - A(W+F)} {W(W+F)} + \frac{-BW+B(W+G)}{W(W+G)}$

$= \frac{-AF}{W(W+F)} + \frac{BG}{W(W+G)}$

$= \frac{1}{W} ( \frac{BG}{W+G} - \frac{AF}{W+F})$

In the problem at hand, there are relations between $W, F, G$

$W = 1 -\delta$
$F = \delta \epsilon_1 = (1-W)\epsilon_1$
$G = \delta \epsilon_2 = (1-W)\epsilon_2$

Substituting in selected places for $F$ and $G$

$L = \frac{1}{W}( \frac{B(1-W)\epsilon_2}{W+G} - \frac{A(1-W)\epsilon_1}{W+F} )$

$= \frac{1-W}{W} ( \frac{ \epsilon_2 B}{W+G} - \frac{\epsilon_1 A}{W+F})$

$= \frac{1-W}{W} ( \frac{ (W+F)\epsilon_2 B - (W+G)\epsilon_1A}{(W+G)(W+F)})$

In the problem at hand:
$A = \prod_{s1}$
$B = \prod_{s2}$
$W = (1 -\delta)$
$F = \delta \epsilon_{s1}$
$G = \delta \epsilon_{s2}$
$\epsilon_1 = \epsilon_{s1}$
$\epsilon_2 = \epsilon_{s2}$.

Thanks so much! The simplification of L makes sense. Could you please dwell on how to separate $( \frac{A}{W} - \frac{B}{W})$ from $( \frac{A}{W + F} - \frac{B}{W + G})$?

 

[Stephen Tashi]

. Could you please dwell on how to separate $( \frac{A}{W} - \frac{B}{W})$ from $( \frac{A}{W + F} - \frac{B}{W + G})$?

I'm not sure what you are asking.

 

[Alec V]

I'm not sure what you are asking.

So, we expressed $( \frac{A}{W + F} - \frac{B}{W + G})$ as $( \frac{A}{W} - \frac{B}{W}) \ + \ L$. You then proceed to further simplify the leftover stuff. However, how can we get from $( \frac{A}{W + F} - \frac{B}{W + G})$ to $( \frac{A}{W} - \frac{B}{W}) \ + \ L$?

Thanks.

 

[Stephen Tashi]

However, how can we get from $( \frac{A}{W + F} - \frac{B}{W + G})$ to $( \frac{A}{W} - \frac{B}{W}) \ + \ L$?

I just defined $L$ to be $( \frac{A}{W + F} - \frac{B}{W + G}) - ( \frac{A}{W} - \frac{B}{W})$