How to derive a differential equation of a first order circuit

[spoonjabba]

Behaviour of any first-order circuit can be described by a first-order ordinary differential equation (often called the state equation) of the form :
dx/dt + αx = βy(t); x(0) = x0
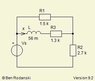
where x is the state variable (usually the voltage across a capacitor or the current across an inductor), y(t) is a voltage or a current source, and the coefficients α, β are constants, depending on circuit elements. Assuming zero initial conditions in the circuit shown below:
1. Derive symbolic expressions for the coefficients α and β in the state equation.
2. If vs(t) = 35·u(t) V, calculate (numerically) the value of the inductor current x at t = 27 µs.

I understand how to derive the expression for a simple RC

dv/dt + v/RC = Vu(t)/dt which is the source

which is just kcl from the node above the capacitor

but for this circuit i have attached I am a bit confuse as to where i should start? should i be zeroing sources? assuming the circuit is in steady state? mesh nodal thevenins nortorns ? any help will be appreciated.

 

[Valkarie]

Answer:1. The coefficients α and β can be derived by using the expression for a first-order ordinary differential equation: dx/dt + αx = βy(t). In this case, the state variable x is the inductor current and y(t) is the voltage source, vs(t). Thus, α is the ratio of the inductance, L, to the capacitance, C, and β is equal to one: α = L/C and β = 1.2. To calculate the value of the inductor current at t = 27 µs, we use the state equation, dx/dt + (L/C)x = 35·u(t), which is a first-order linear differential equation. We can solve this equation by using the method of integrating factors, which yields the following solution: x(t) = x0 + 35·e^(-(L/C)·t) where x0 is the initial condition at t = 0. Substituting t = 27 µs and the given values of L and C into the equation yields x(27 µs) = x0 + 35·e^(-27/(L·C)).