LightPhoton
- 42
- 3
- TL;DR Summary
- I ask about how one can use generalized STE to motivate momentum operator in position basis using the approach of Griffiths and Schroeter
I am not able to use Latex for some reason. It is very glitchy and if I do one backspace then it fills my whole screen with multiple copies of the same equation. Thus I am pasting a screenshot of handwritten equations instead. Apologies for any inconvenience.
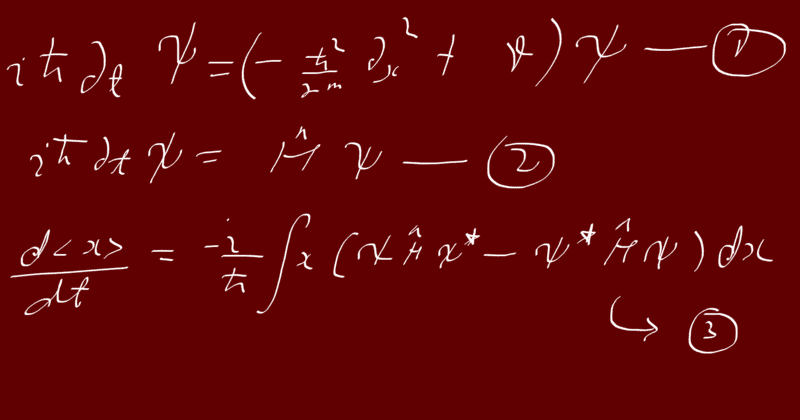
In Introduction to Quantum Mechanics by Griffiths and Schroeter, the IMO motivates the form of momentum operator in position basis in a very nice manner. However, the problem is that they use a very specific form of STE (1)
Instead, I want to work in a much more general setting by writing STE as (2)
Now, the authors motivate it by taking time derivative of the expectation value of the position, which leads me to (3).
However, I am not sure how to proceed from here.
In Introduction to Quantum Mechanics by Griffiths and Schroeter, the IMO motivates the form of momentum operator in position basis in a very nice manner. However, the problem is that they use a very specific form of STE (1)
Instead, I want to work in a much more general setting by writing STE as (2)
Now, the authors motivate it by taking time derivative of the expectation value of the position, which leads me to (3).
However, I am not sure how to proceed from here.