I How to derive the energy of a parabolic confining potential in a wire

[john chen]

Hi all,

How to derive the energy of a parabolic confining potential in a wire as shown below? I tried to follow the derivation of the harmonic, oscillator like we did for the quantum well and the magnetic field but i can't find anything that has an expression that come close to the one shown below.

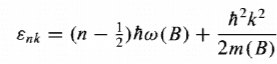where

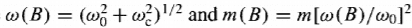
I really have no idea how to start and i really appreciate if anybody is willing to guide me or help me. Thanks...

 

[stevendaryl]

Did the book explicitly give a hamiltonian for the particles in the wire?

 

[hutchphd]

Do you know how to incorporate a Magnetic Vector Potential into the Hamiltonian?

 

[john chen]

Hi all, thanks for replying! @stevendaryl The book doesn't really give a hamiltonian for the particles in the wire but its gives a SHO equation in landau gauge which gains confining potential

which I am not sure can it be used in pkace of that?

@hutchphd I have never done anything related to magnetic vector potential into hamiltonian so far so if is really needed, i would like to know how is it done..Anyways the link to the equation for energy of confining parabolic potential can be found in this link http://macbeth.if.usp.br/~gusev/Davies.pdf page 249, equation 6.53

 

[hutchphd]

@hutchphd I have never done anything related to magnetic vector potential into hamiltonian so far so if is really needed, i would like to know how is it done..

I see that he gives you the form for the parabolic"magnetic" confinement just before 6.53 so you don't really need to go to Vector potential (any quantum text will have it if you are interested). So put that into V(x) in 6.52 and regroup terms using the definitions immediately after 6.53. It should then look like the 2D SHO in directions perpendicular to wire axis. Therefore you can write down the eigenvalues using these new definitions which contain the parameter B to obtain 6.53. The k is along the wire axis

 

[john chen]

@hutchphd @stevendaryl So is V(x) = mw0x^2/2 or the one that is circled in blue below equation 6.52? Because I went to spend a few hours using V(x) = mw0x^2/2 into equation 6.52

but to no avail I can't link it to the definitions

.

 

[john chen]

And do I have to introduce an expression for wave function u(x) to solve for the energy of confining parabolic potential?

 

[hutchphd]

Yes he does redefine the zero point for x as you point out ( I missed that), express the potential using (x-x_k ) and consolidate terms.

And do I have to introduce an expression for wave function u(x) to solve for the energy of confining parabolic potential?

You need only to then say "hey, this is exactly a SHO Hamiltonian with a redefined origin for x and a funny mass etc" and write down the known corresponding solution for whatever you need.

 

[john chen]

@hutchphd ah I see, so I do still use V(x) = mw0x^2/2 for equation 6.52? Anyways thanks for helping, really appreciate!

 

[hutchphd]

@hutchphd ah I see, so I do still use V(x) = mw0x^2/2 for equation 6.52? Anyways thanks for helping, really appreciate!

It should be quadratic in (x-x_k) and expressed using w₀ I think. You can make it work.