- #1
PainterGuy
- 940
- 70
Hi,
I was trying to solve the following problem myself but couldn't figure out how the given Taylor series for log(x) is found.
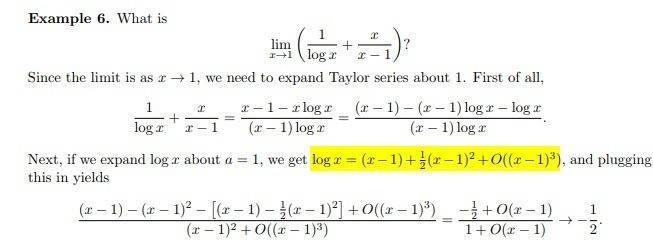
Taylor series for a function f(x) is given as follows.
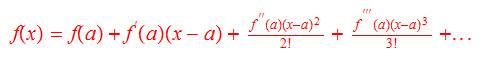
Question 1:
I was trying to find the derivative of log(x).
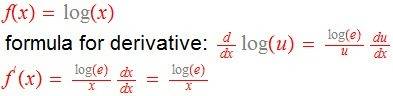
My calculator gives it as d{log(x)}/dx=1/In(x)*x.
How do I convert log(e)/x to 1/In(x)*x? Logarithm base change formula isn't working for me. Thank you for your help!
I was trying to solve the following problem myself but couldn't figure out how the given Taylor series for log(x) is found.
Taylor series for a function f(x) is given as follows.
Question 1:
I was trying to find the derivative of log(x).
My calculator gives it as d{log(x)}/dx=1/In(x)*x.
How do I convert log(e)/x to 1/In(x)*x? Logarithm base change formula isn't working for me. Thank you for your help!
Attachments
Last edited:


