How to determine drain-source voltage for this MOSFET amplifier.

[zenterix]

TL;DR Summary: I took a few hours to come up with the solution below. The problem isn't the math or anything, but rather the concepts involved. We are asked to find the relationship between two voltages in a MOSFET operating under different conditions.

The MOSFET in the circuit below is characterized by the equation $i_{DS}=\frac{K}{2}(v_{GS}-V_T)^2$ in its saturation region according to the SCS model. The MOSFET operates in the saturation region for $v_{GS}\geq v_{GS}-V_T$ and $v_{GS}\geq V_T$. Suppose the MOSFET is characterized by the SR model in its triode region. In other words, $i_{DS}=\frac{v_{DS}}{R_{ON}}$ in the triode region.

Assume that $R_{ON}$ is constant with respect to $i_{DS}$ and $v_{DS}$, but its value is some function of $v_{GS}$. Further suppose that $i_{DS}=0$ when $v_{GS}<V_T$.

a) For $v_{GS}=5\text{V}$, what value of $R_{ON}$ makes the MOSFET $i_{DS}$ versus $v_{DS}$ characteristic continuous between its triode and saturation regions of operation?

b) Plot $v_R$ versus $v_D$ for the circuit shown below. This circuit is useful in plotting the MOSFET characteristics. Assume that $K=1\mathrm{mA/V^2}$ and $V_T=1\text{V}$. Use the value of $R_{ON}$ calculated in (a). Use a volt scale for $V_D$ and a millivolt scale for $v_R$.

Consider the following circuit

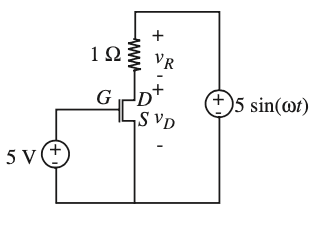
If $v_{GS}=5\text{V} > 1\text{V}=V_T$ and $v_D<v_{GS}-V_T=5-1=4\text{V}$ then the MOSFET is in an ON state (ie, closed state) and is operating in the triode region of its i-v plot. That is, it behaves as a linear resistor with resistance $R_{ON}$.

If, on the other hand, $v_D>v_{GS}-V_T=4\text{V}$ then the MOSFET operates in the saturation region and the current though it is fixed given $v_{GS}=5\text{V}$.

For part a) of this problem, all we have to do is make sure that the end of the triode region (where $v_D=v_{GS}-V_T=4\text{V}$), represented by $i_D=\frac{4\text{V}}{R_{ON}}$, equals the beginning of the saturation region, represented by $i_D=\frac{K(v_{GS}-V_T)^2}{2}$.

Solving for $R_{ON}$ we obtain $R_{ON}=\frac{2}{K(v_{GS}-V_T)}$.

My questions are about part b).

Using the result of part a), we can compute $R_{ON}=500\Omega$.

Given $v_{GS}=5\text{V}$, the MOSFET is in an ON state, and it seems that $v_D$ oscillates in some interval within the range $-5\text{V}$ and $5\text{V}$ (because $-5\leq 5\sin{(\omega t)}\leq 5$).

When we are in the saturation region then we have $i_{DS}=\frac{1\mathrm{\frac{mA}{V^2}}(5V-1V)^2}{2}=8\text{mA}$ which we can equate to $\frac{v_R}{1\Omega}$ and so $v_R=8\text{mV}$.

Suppose we call the sinusoidal voltage on the right $v_S$. Let's consider first only positive values for this voltage.

Using KVL we have

$-V_S+v_R+v_D=0$

$v_D=V_S-v_R=5\sin{(\omega t)}-8\text{mV}$

which is true as long as we are in saturation, ie $v_D>4V$ ie $\sin{(\omega t)}>\frac{4.008}{5}\approx 0.8V$ and $0.93 \text{rad}\leq \omega t \leq \pi-0.93\text{rad}$.

So it seems that as long as we are in saturation region, $v_R$ is fixed and $v_D$ changes in time and is between $4\text{V}$ and $4.992\text{V}$.

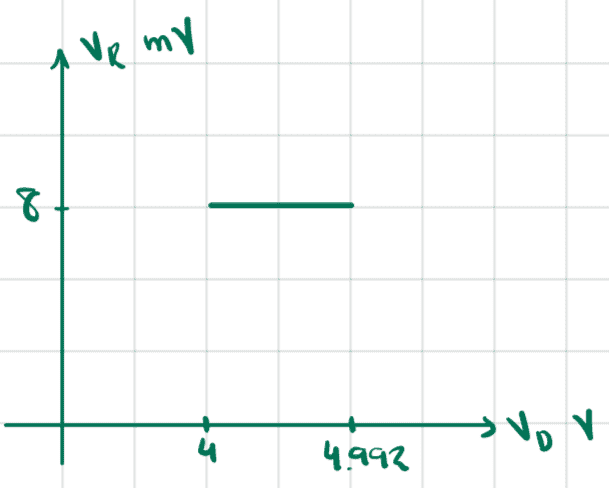
Considering only positive $v_D$, when the condition $v_D>4$ is not met we are in the triode region, in which the MOSFET behaves like a linear resistor.:

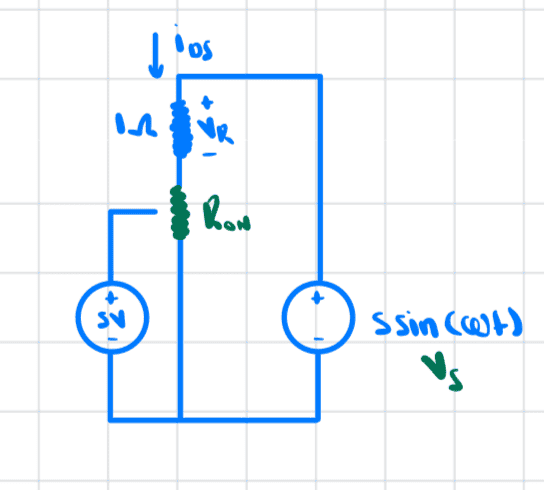
We know what $R_{ON}$ is by using the expression from part a): $R_{ON}=500\Omega$.

We can now determine the current $i_D$ and the voltages across each resistor.

$v_R = \frac{1}{501}5\sin{(\omega t)}$

$v_D = \frac{500}{501}5\sin{(\omega t)}$

$i_D=\frac{5\sin{(\omega t)}}{501}$

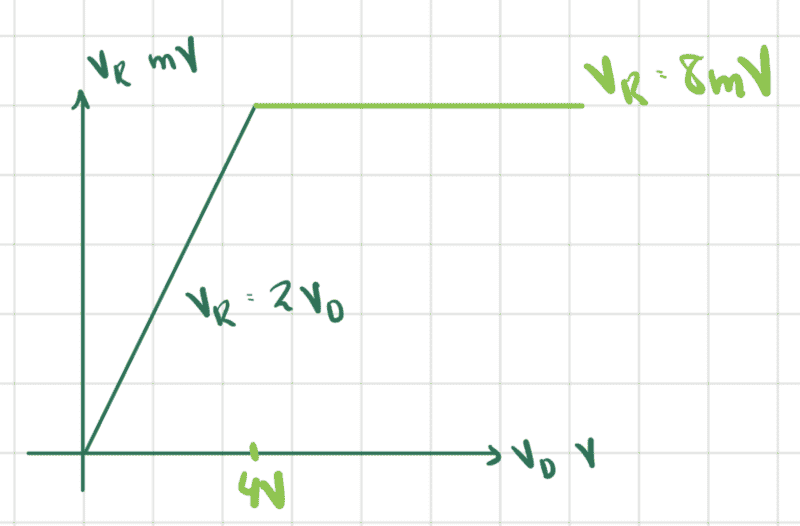
The relationship of $v_R$ with $v_D$ is then given by $v_R=\frac{1}{500}v_D$ where both variables are in volts, and if we measure $v_R$ in $mV$ then we have $v_R=2v_D$, which we plot as

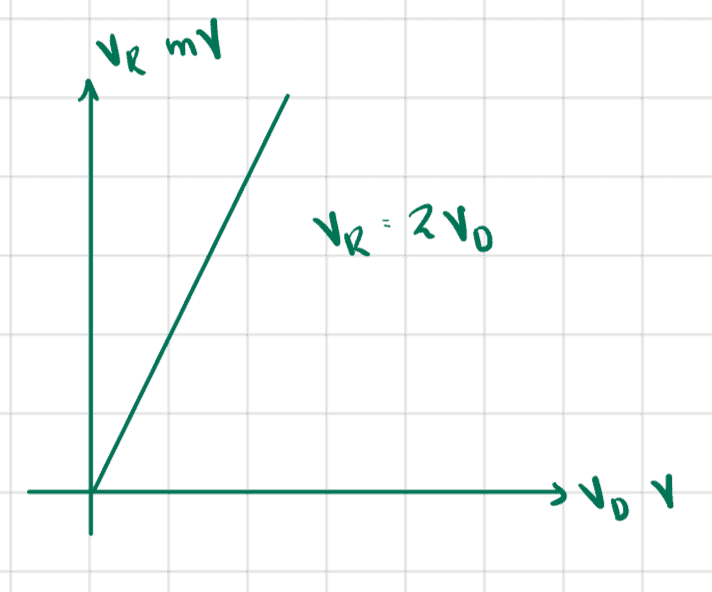
Is this analysis correct and would the analysis when $V_S=5\sin{(\omega t)}<0$ be similar?

If we plot the relationship for all positive values of $v_D$ then it seems that we get