How to determine natural boundary condition and essential b.c. in Ritz method

[omer21]

I am trying to understand Ritz method, but i have troubles wtih determining the boundary conditions. After weak formulation of a differential equation how do we determine natural and essential b.c.?

What are boundary terms, secondary variables, primary variables, natural and essential boundary conditions exactly?
Can somebody explain these terms please?

For example

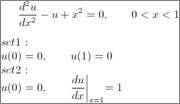
in above differential equation, what are boundary terms, secondary variables, primary variables, natural and essential boundary conditions?

 

[gtoguy97]

In order to answer this question, you need to break down the components of the differential equation. The boundary terms are the parts of the equation that impose a specific boundary condition, such as a Dirichlet or Neumann condition. Secondary variables are any additional variables used to solve the equation, such as an auxiliary variable. Primary variables are the dependent and independent variables in the equation, such as displacement, force, time, etc. Natural and essential boundary conditions refer to the type of boundary condition imposed on the problem. Natural boundary conditions are those that are imposed by the physical nature of the problem, such as an applied force or a fixed displacement at a certain location. Essential boundary conditions are those that are imposed by the mathematical formulation of the problem, such as a Neumann or Dirichlet condition.