mathdad
- 1,280
- 0
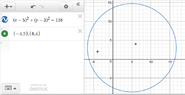
Determine the equation of the circle in standard form, given the coordinate of the diameter PQ.
P(-4, -2) and Q(6, 4)
Midpoint is (5, 3).
d = sqrt{(6-(-4))^2 + (4-(-2))
d = sqrt{(10)^2 + (6)^2}
d = sqrt{100 + 36}
d = r = sqrt{136}
Let d = distance = radius
(x - h)^2 + (y - k)^2 = r^2
(x - 5)^2 + (y - 3)^2 = [sqrt{136}]^2
(x - 5)^2 + (y - 3)^2 = 136
Correct?
P(-4, -2) and Q(6, 4)
Midpoint is (5, 3).
d = sqrt{(6-(-4))^2 + (4-(-2))
d = sqrt{(10)^2 + (6)^2}
d = sqrt{100 + 36}
d = r = sqrt{136}
Let d = distance = radius
(x - h)^2 + (y - k)^2 = r^2
(x - 5)^2 + (y - 3)^2 = [sqrt{136}]^2
(x - 5)^2 + (y - 3)^2 = 136
Correct?