How to differentiate 1/y without making a fundamental mistake?

[grace77]

Problem statement
Find dy/dx

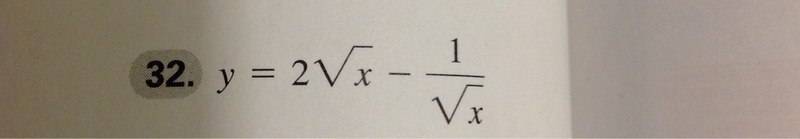
Revelant equations
None

Attempt at a solution

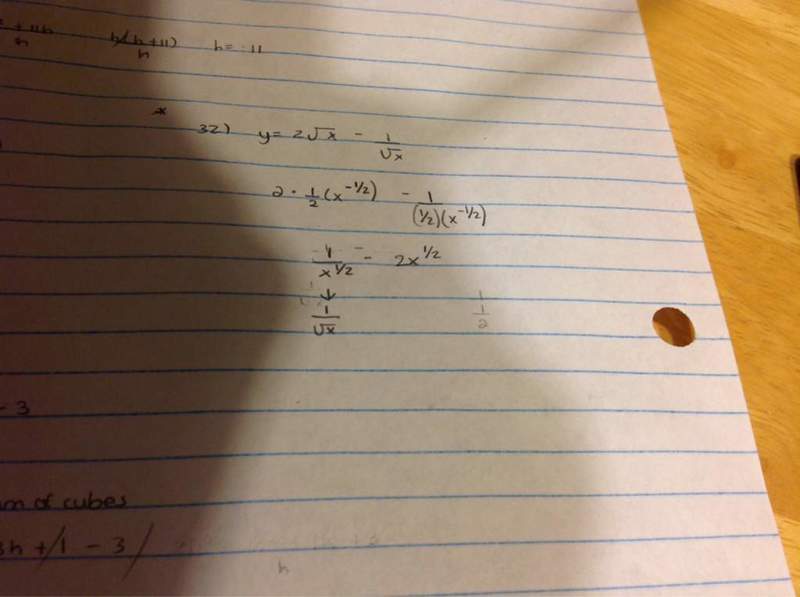
This is what I got to so far but now I'm stuck... Any hints?

 

[BvU]

Do you think you can use the template from now on ?
You need at least one relevant equation, and it is not clear to me what you do in your aattempt. Could you elaborate ?

 

[SteamKing]

It would be less confusing if you wrote y using exponents before doing the differentiation. Check the derivative of the second part of your expression; I think you have an error in the sign.

 

[grace77]

It would be less confusing if you wrote y using exponents before doing the differentiation. Check the derivative of the second part of your expression; I think you have an error in the sign.

Yes I think I put a negative 1/2 should be a positive

 

[grace77]

Do you think you can use the template from now on ?
You need at least one relevant equation, and it is not clear to me what you do in your aattempt. Could you elaborate ?

Ok I am not sure what equation to use in this though.

 

[HallsofIvy]

You are making a fundamental mistake: the derivative of 1/y is NOT 1 over the derivative of y. Either use the quotient rule to differentiate \frac{1}{\sqrt{x}} or write the whole function as 2x^{1/2}+ x^{-1/2} and use the derivative rule (x^n)'= nx^{n-1}.

 

[grace77]

You are making a fundamental mistake: the derivative of 1/y is NOT 1 over the derivative of y. Either use the quotient rule to differentiate \frac{1}{\sqrt{x}} or write the whole function as 2x^{1/2}+ x^{-1/2} and use the derivative rule (x^n)'= nx^{n-1}.

Thank you I understand it now