How to Disprove a Nested Quantifier Expression?

[albert1992]

I have trouble disproving the following expression

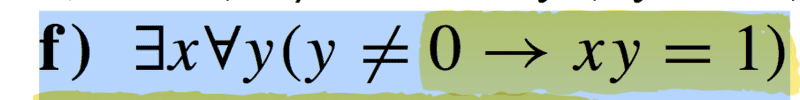
I worded it as follows:

The product of certain number and every other nonzero number is 1

 

[Bashyboy]

First of all, does the problem specify what the domain is for x and y?

To start, let's back things up a bit. In mathematical terms, the statement is as follows: There exists an x for every possible y value, such that if y isn't zero, when you choose an x-value, you can multiply it by every y-value in the domain, and the result is 1. So, assuming the domain is real numbers, for both x and y, let's try choosing a value for x:

Let x = 5. What value of y would make the statement true? y = 1/5. So, we've tested JUST ONE y-value. x = 5 has to work for EVERY single y. Can you think of a y-value that would make the statement false?EDIT: If anyone thinks my reply contains fallacious ideas, please inform me.

 

[Bashyboy]

@Albert, has my reply stirred any thoughts in your mind?