How to Divide by 9 and Find Remainders

  • Thread starter jim1174
  • Start date
So, we can say that 9 goes into 24 2 times with a remainder of 6. In summary, to solve the problem, we first divide 9 into 44, getting a quotient of 4 and a remainder of 8. Then, we bring down the 3 and divide 9 into 83, getting a quotient of 9 and a remainder of 2. Finally, we bring down the 4 and divide 9 into 24, getting a quotient of 2 and a remainder of 6. This pattern continues until there are no more numbers to bring down.
  • #1
jim1174
79
0
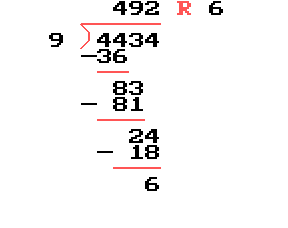
I got this problem off the internet and need some help understanding how to do it. first you do 9 goes into 44 4 times so you put a 4 on top then you do 9 times 4 equals 36 so you put the 36 under the 44. next you do 44 minus 36 which is 8 and bring down the 3. can you please explain how to get the other numbers in the problem ?
jimm.gif
 
Mathematics news on Phys.org
  • #2
If I tell you that 9 goes into 83 9 times, can you take it the rest of the way?
 
  • #3
ok so where does the 2 on the top come from ?
 
  • #4
9 x 9 = 81, subtract that from the 83, gives you 2, bring down the 4 -----
Starting to see the pattern?
 
  • #5
yes i understand that part but how do you get the 2 on the top next to the 49
 
  • #6
9 goes into 24 2 times
 
  • #7
9*2= 18< 24< 27= 9*3

Since "9*3" is too large, we take "2" leaving a remainder of 24- 18= 6.
 

FAQ: How to Divide by 9 and Find Remainders

1. How do I approach a complex problem?

The first step is to break down the problem into smaller, more manageable parts. Then, analyze each part individually and see how they relate to the overall problem. This will help you form a strategy for solving the problem.

2. What if I get stuck while trying to solve a problem?

It's common to get stuck while solving a problem. Take a step back and try to look at the problem from a different angle. You can also seek help from a peer or a mentor to get a fresh perspective.

3. How do I know which equations/formulas to use for a problem?

Read the problem carefully and identify what information is given and what is being asked. Then, use your knowledge of the subject and relevant equations/formulas to determine the best approach for solving the problem.

4. What if I make a mistake while solving a problem?

Mistakes are a natural part of problem-solving. If you realize you made a mistake, go back and retrace your steps to find where you went wrong. Double-check your calculations and make any necessary corrections.

5. How do I know if my solution to a problem is correct?

Once you have solved the problem, double-check your work and make sure all of your calculations are correct. Then, check if your solution makes sense in the context of the problem. If it does, then you have likely found the correct solution.

Similar threads

MHB Not a "help need" but a question about "a self made square root formula"
Replies
2
Views
2K
Find the remainder when ## 4444^{4444} ## is divided by ## 9 ##.
Replies
3
Views
2K
I Probability to get a certain number or less by throwing two 6-faced die
Replies
6
Views
2K
MHB Vatha & Chris Ages: Solve to Find Out How Old They Are Now
Replies
1
Views
2K
B Dividing the jewel maker's diamonds -Riddle (Easy)
Replies
2
Views
1K
B Intermediate Value Theorem and Synthetic Division
Replies
4
Views
2K
I Find an explicit formula for this n-sum problem
Replies
7
Views
2K
MHB What is the Probability of Winning a Dice Game?
Replies
1
Views
2K
MHB How Can One Demonstrate the Ratio Between the Hypotenuses of Two Triangles?
Replies
2
Views
2K
MHB Help with Probability, Roulette, and Population Statistics
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top