greypilgrim
- 579
- 44
Hi.
I can calculate the expectation values in the Bell (or in this case, CHSH) inequality and show that they violate it for entangled particles. But I'm confused about how to calculate them for an actual sequence of measurements, which could look like this ("Paar" is for photon pair):
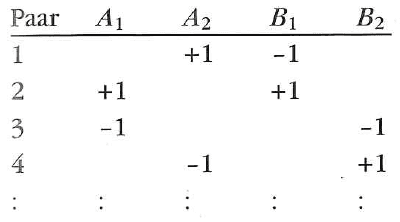
How do i now calculate from this the expectation values in
##\langle A_1 B_1 \rangle+\langle A_1 B_2 \rangle+\langle A_2 B_1 \rangle-\langle A_2 B_2 \rangle\ ?##
For example, how do I calculate ##\langle A_1 B_1 \rangle## for for the pairs 1, 3 and 4 where Alice's or Bob's detector where at setting 2? Or do I only consider cases like pair 2 for this?
I can calculate the expectation values in the Bell (or in this case, CHSH) inequality and show that they violate it for entangled particles. But I'm confused about how to calculate them for an actual sequence of measurements, which could look like this ("Paar" is for photon pair):
How do i now calculate from this the expectation values in
##\langle A_1 B_1 \rangle+\langle A_1 B_2 \rangle+\langle A_2 B_1 \rangle-\langle A_2 B_2 \rangle\ ?##
For example, how do I calculate ##\langle A_1 B_1 \rangle## for for the pairs 1, 3 and 4 where Alice's or Bob's detector where at setting 2? Or do I only consider cases like pair 2 for this?