How to estimate the heating of a wire

[decaf14]

TL;DR

How to estimate heating of a wire

Hello,

I've done some background research on this, and answers seem to vary. I would like to calculate the amount of heating in a wire. Let's say I want to heat a wire up to 60 degrees. I have 1 W of power and 150 mA of current at my disposal to do so. How could I estimate the wire diameter required for this?

Here are my thoughts based on what I've read: there is no easy analytical expression, but I have two expressions at my disposal. One for resistance of a wire given length, resistivity, and cross sectional area. The other would simply be power: P = I^2 * R

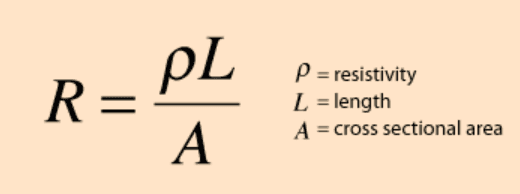
These equations would allow me to calculate perfectly the wire diameter and length for a certain power dissipation. However, I would not know how to relate this to temperature rise.

The other option, which I'm more tempted to do at this point, would be to create a power vs. temperature curve for certain diameter wire using a microcontroller.

 

[anorlunda]

You are missing the part about heat dissipation to the environment.

Obviously these three cases yield different temperatures for the same power.

1. an insulated wire in still air
2. a bare wire in moving air
3. a wire immersed in water

 

[decaf14]

You are missing the part about heat dissipation to the environment.

Obviously these three cases yield different temperatures for the same power.

1. an insulated wire in still air
2. a bare wire in moving air
3. a wire immersed in water

Ahh, yes. Let's assume we are working with air, then. I'm still struggling to find an equation I can apply to this system. My closest guess is the specific heat equation, Q = m*c*dT. I could calculate the mass of the wire based on it's dimensions, then input the specific heat constant. The issue with this equation is that it implies a linear increase in energy will yield a linear increase in temperature. This is not the case, as ~10k resistors in our mobile devices can be used indefinitely without extra heating. The equation does not account for dissipation.

If I were to account for dissipation, I figure I'd have to pick a mass for air. However, my air is a "sink" and has technically infinite mass, which does not play well with this equation. The air is like a boundary condition.

 

[anorlunda]

Specific heat relates the energy stored in the material. In your case, heat generated must equal heat lost to the environment in the long term. Energy stored in the materials is so small as to be negligable.

Rather than specific heat, you need the heat transfer coefficient. That is very difficult to calculate, and it is usually found by experiment.

But if you want to calculate, this question has been discussed before. It's not simple. Heat is lost by conduction, convection and radiation.

Since we have not sufficient data to calculate I have to improvise some.
I think the wire diameter will be 0.097" and ρ≈ 1 ohm*mm^2/m at 21oC and temperature factor 0.123. The resistance at 21.1oC[70oF] will be 0.214 ohm and 1.9 at 85.11 oC.[185.2oF instead of 128.5!].
The 3 rows of insulating tape will add another 6*0.005=0.030" and the final overall diameter will be 0.127".
According to Neher&McGrath [these formulae were revised in IEEE-835/1994] convection evacuation power will be:
Wc=0.072*Ds ^0.75*∆T^1.25*length[ft] (eq. 56)
Let's say Ts=82oC [outside surface temperature] then ∆T=61oC and then Wc=7.83 W.
Radiation:
Wr=0.10256*Ds*ε*∆T*[1+0.0167*Tm] [eq.55a] Wr=4.08 [W]
Total evacuated power =Wc+Wr=11.91 W
Conduction it could be from this wire to the battery, ampermeter and voltmeter connection 13.15-11.91=1.24 W.
This it could be a 1.43 ft 0.5 mm^2 copper conductor 0.5 mm insulation thickness at 60oC[average].[Wc=0.887 W;Wr=0.356 W]

But many people avoid directly calculating temperature, and work with ampacity instead.

Ampacity is the maximum current that a conductor can carry continuously under the conditions of use without exceeding its temperature rating. Current is measured in amperes or “amps”. You must use the correct size wire for the current (load) requirement of the circuit to prevent the wire from overheating.

That link provides a chart giving the maximum amps for different wire sized and a 60C temperature rating,

 

[decaf14]

Specific heat relates the energy stored in the material. In your case, heat generated must equal heat lost to the environment in the long term. Energy stored in the materials is so small as to be negligable.

Rather than specific heat, you need the heat transfer coefficient. That is very difficult to calculate, and it is usually found by experiment.

But if you want to calculate, this question has been discussed before. It's not simple. Heat is lost by conduction, convection and radiation.But many people avoid directly calculating temperature, and work with ampacity instead.That link provides a chart giving the maximum amps for different wire sized and a 60C temperature rating,

Thanks for this! Ampacity was the keyword I needed. I had seen these charts before, but they were rated for 30 C. 60, 75, and 90 seems far more useful. I'll engineer around this as a rough estimate and better hone in on actual temperature rise experimentally.

 

[Babadag]

anorlunda said:But many people avoid directly calculating temperature, and work with ampacity instead.

.

I agree with anorlunda. However, the standard ampacity table[as per NEC] -or current carrying capacity in IEC World- are only for copper and aluminum 14 awg minimum conductor cross section area [see for instance Table 310.15(B)(17) (formerly Table 310.17) Allowable Ampacities of Single-Insulated Conductors Rated Up to and Including 2000 Volts in Free Air, Based on Ambient Temperature of 30°C (86°F)* and current from 25 A.

If the wire length it is not more than 10 fts. in order to achieve 45 ohm [for 1W at 0.15 A] at 60oC you have to use a 2 mils diameter aluminum [less than 36 awg]. Calculation is necessary for any exception not included in standard ampacity table. In your case a nickel chrome wire it is more practical.