- #1
Gourab_chill
- 55
- 3
- Homework Statement
- I've got the question in the attachments. I've got doubt regarding the expansion of 1+x^n
- Relevant Equations
- i don't know the expansions
I could simplify the expressions in the numerator and denominator to (1+x^n)/(1+x) as they are in geometric series and I used the geometric sum formula to reduce it. Now for what value of n will it be a polynomial?
I do get the idea for some value of n the simplified numerator will contain the (1+x) factor in it. What sort of expansion or formula should be used here?
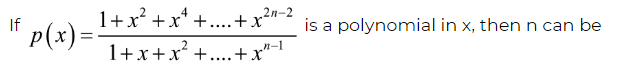
I do get the idea for some value of n the simplified numerator will contain the (1+x) factor in it. What sort of expansion or formula should be used here?
Last edited by a moderator:
 )
)