- #1
cognosco123
- 1
- 0
The problem is attached.
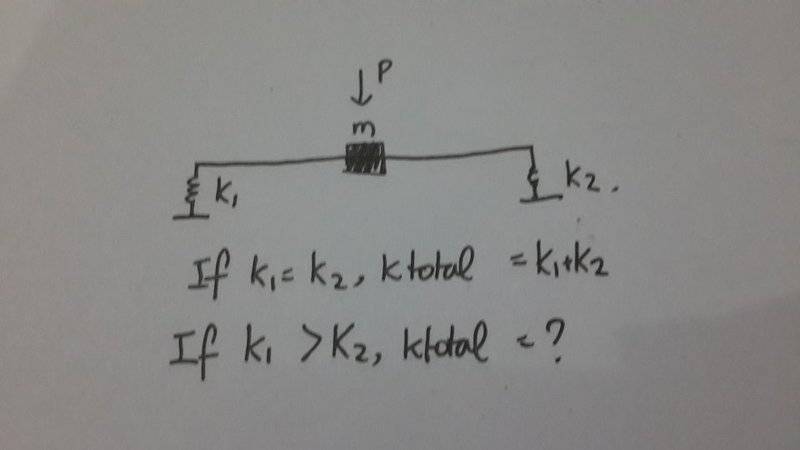
I'll disagree on this. The parallel springs formula assumes that both springs displace the same. Here, however, the springs will displace differently to maintain equilibrium. Therefore, a unique formula needs to be derived.Daniel Sadlier said:
The beam spring stiffness coefficient can be calculated by dividing the load (force applied to the beam) by the deflection (amount the beam bends). This calculation can be represented by the equation k = F/d, where k is the stiffness coefficient, F is the applied load, and d is the deflection.
The beam spring stiffness coefficient is affected by the material properties of the beam, such as its Young's modulus and cross-sectional area. The geometry of the beam, including its length and thickness, also plays a role in determining the stiffness coefficient. Additionally, the type of loading and support conditions can impact the stiffness coefficient.
No, the formula for calculating stiffness coefficient may vary depending on the type of beam and its loading and support conditions. For example, a cantilever beam will have a different formula for calculating stiffness compared to a simply supported beam.
The deflection of a beam can be measured using a variety of methods, including strain gauges, displacement sensors, and deflection gauges. These tools can be attached to the beam and used to measure the amount of bending or displacement under a given load.
Yes, the beam spring stiffness coefficient can be changed by altering the material properties, geometry, or support conditions of the beam. For example, increasing the cross-sectional area of the beam or using a stiffer material can result in a higher stiffness coefficient.