PeaceMartian
- 2
- 2
New poster has been reminded to show their work when posting schoolwork type questions
TL;DR Summary: How to find integrals of parent functions without any horizontal/vertical shift?
Say you were given the equation :
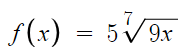
How would you find :
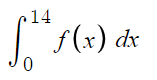 with a calculator that can only add, subtract, multiply, divide
with a calculator that can only add, subtract, multiply, divide
Is there a general formula?
Say you were given the equation :
How would you find :
Is there a general formula?