Mohmmad Maaitah
- 90
- 20
- Homework Statement
- find range
- Relevant Equations
- none
Hi, so I know how to find domain but how about range in this problem?
I don't understand the way he did it?
I always get answers wrong when it comes to range.
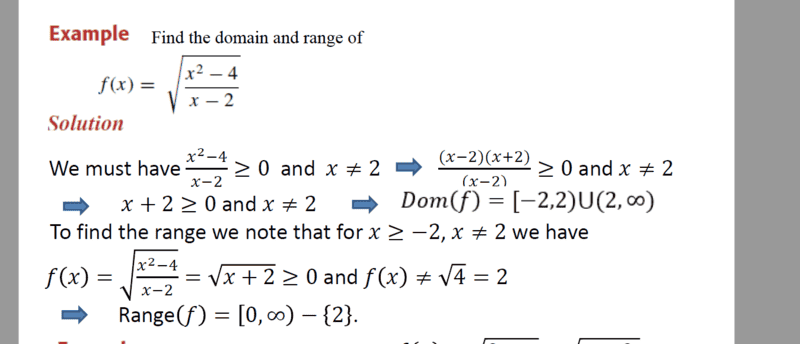
I don't understand the way he did it?
I always get answers wrong when it comes to range.