How to Find the Area of Quadrilateral ABCD with Given Side Lengths and Angles?

[Albert1]

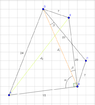
$Quadrilateral\,\,ABCD,\overline{AB}=15,\overline{AD}=24,\overline{BC}=7,\overline{CD}=20, \,\,
\angle ABD+\angle BDC=90^o\,\,
find \,\, the \,\, area\,\, \,\, of \,\, ABCD$

 

[lfdahl]

My suggested solution:

Spoiler

View attachment 6350$\bigtriangleup BCD$ is replaced by its mirror image $\bigtriangleup BED$. $\angle ABE$ is then $90^{\circ}$.Length of diagonal $d_2$ is: $\sqrt{15^2+20^2} = 25$.The total area of the quadrilateral can now be calculated:Area of $\bigtriangleup ABE$ + Area of $\bigtriangleup AED$ (Herons formula with perimeter $56$) $= 150+84 = 234$.

 

[Albert1]

My suggested solution:

Spoiler

$\bigtriangleup BCD$ is replaced by its mirror image $\bigtriangleup BED$. $\angle ABE$ is then $90^{\circ}$.Length of diagonal $d_2$ is: $\sqrt{15^2+20^2} = 25$.The total area of the quadrilateral can now be calculated:Area of $\bigtriangleup ABE$ + Area of $\bigtriangleup AED$ (Herons formula with perimeter $56$) $= 150+84 = 234$.

nice solution !