How to find the deceleration of a mass colliding on a spring?

[k.udhay]

Homework Statement

A known mass at a know velocity collides on a spring of known stiffness. What is the equation that governs the deceleration of the mass, so that the force on the spring could be found?

Relevant Equations

1/2 m*V^2 = 1/2*k*x^2 + 1/2*m*(Vo)^2

Kinetic energy of mass before collision = Potential energy of spring at an instance + Kinetic energy of mass at the same instance

Problem Statement: A known mass at a know velocity collides on a spring of known stiffness. What is the equation that governs the deceleration of the mass, so that the force on the spring could be found?
Relevant Equations: 1/2 m*V^2 = 1/2*k*x^2 + 1/2*m*(Vo)^2

Kinetic energy of mass before collision = Potential energy of spring at an instance + Kinetic energy of mass at the same instance

I am creating a simple mathematical model to understand the impact of a moving object on a sprung system:

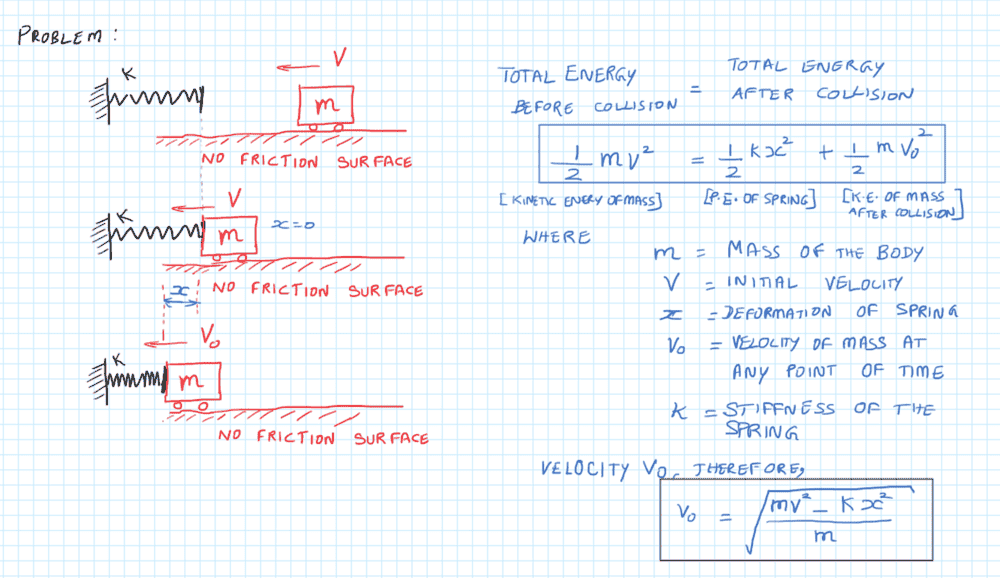As you can find, I am able to find the velocity of the object at any 'x' value after collision. I am also able to figure out the max. 'x' value by equating kinetic energy of the mass on RHS of the equation to zero. I am unable to find out the following though:

1. How to find the position of mass x W.R.R. time?
2. V_o is (dx / dt). I want the acceleration (d²x/dt²). I am out of touch with calculus for a very long time, adding to the fact that maths is my weak subject.

Can someone help me finding the above two points pl.?

 

[BvU]

How to find the position of mass x W.R.R. time"

You use Newton: $F = ma$ in combination with the (ideal) spring equation $F = - kx$

 

[k.udhay]

You use Newton: $F = ma$ in combination with the (ideal) spring equation $F = - kx$

But I don't know either acceleration or x. All I know is the time t.

 

[Abhishek11235]

Hint: F=$\text{m} d^2 x/dt^2 =\text{-kx}$

 

[haruspex]

I am out of touch with calculus for a very long time

Then you are unlikely to be able to solve the differential equation. Have you heard of simple harmonic motion?
Plug in the solution $x=A\sin(\omega t)$, where A and ω are unknown constants and see what happens.

By the way, your use of v and v₀ is confusing. Usual is to have the unsubscripted form for the generic variable and the subscript to denote a particular value of it.

 

[k.udhay]

Then you are unlikely to be able to solve the differential equation. Have you heard of simple harmonic motion?
Plug in the solution $x=A\sin(\omega t)$, where A and ω are unknown constants and see what happens.

By the way, your use of v and v₀ is confusing. Usual is to have the unsubscripted form for the generic variable and the subscript to denote a particular value of it.

Yes, I later realized I should have given the subscripts correctly.