bsmithysmith
- 23
- 0
View attachment 2423
I know the Double Angle for Sine is:
$$\sin(2x) = 2\sin(x) \cos(x)$$
but from the triangle given, how do I figure it out? We did this in class, but the teacher just told a small amount of things, and then let us talk amongst each other to solve it. Nearly all the students were glossy eyed and did not know how to find it.
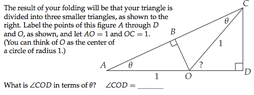
Another question Is how do I find what $\cos(3x)=?$ Same thing but we did it today, and as always, none of the students know how to do it and the teacher didn't seem to help a lot. We had an origami folding paper to help us and made 3 triangles within 3x, so a trisect, if that's what it's called. Still not understanding the triple angle formula, but he did say that it's a combination of $\sin(2x), \sin, \cos(2x),$ or $\cos$; something like that. And he's looking for single thetas (whatever that means).
I know the Double Angle for Sine is:
$$\sin(2x) = 2\sin(x) \cos(x)$$
but from the triangle given, how do I figure it out? We did this in class, but the teacher just told a small amount of things, and then let us talk amongst each other to solve it. Nearly all the students were glossy eyed and did not know how to find it.
Another question Is how do I find what $\cos(3x)=?$ Same thing but we did it today, and as always, none of the students know how to do it and the teacher didn't seem to help a lot. We had an origami folding paper to help us and made 3 triangles within 3x, so a trisect, if that's what it's called. Still not understanding the triple angle formula, but he did say that it's a combination of $\sin(2x), \sin, \cos(2x),$ or $\cos$; something like that. And he's looking for single thetas (whatever that means).