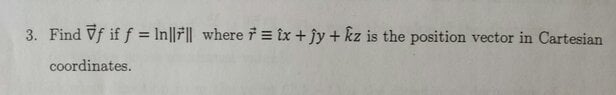How to Find the Gradient of ln|r|?

[Logan Land]

To solve the gradient f when f = ln |r| do I start with differentiating each x,y,z term of the vector?Like ln|x| ln|y|...etc.

View attachment 4146

 

[Logan Land]

(ATTEMPT)

gradient(ln||^r||)

=((d/dx)x*+(d/dy)y*+(d/dz)z*)(ln||r||)
=(x/r^2)x*+(y/r^2)y*+(z/r^2)z*
=(x,y,z)/r^2
=(^r)/r^2

correct?

 

[Fantini]

Notice that $\ln(\| {\mathbf r} \|) = \ln (\sqrt{x^2+y^2+z^2})$. You need to use the chain rule for the gradient. I don't understand your notation. :(

 

[Logan Land]

Notice that $\ln(\| {\mathbf r} \|) = \ln (\sqrt{x^2+y^2+z^2})$. You need to use the chain rule for the gradient. I don't understand your notation. :(

i tried to follow how I attempted the next question, gradient f if f=1/r
(d/dx)xbar+(d/dy)ybar+(d/dz)zbar * (1/r)
(-x/r^3)xbar+(-y/r^3)ybar+(-z/r^3)zbar
= -(x,y,z)/r^3
=-rbar/r^3thats how I tried but I guess was wrong?

 

[Logan Land]

d/dx ln(sqrt x^2+y^2+z^2) = x/(x^2+y^2+z^2) d/dy = y/(x^2+y^2+z^2) and d/dz = z/(x^2+y^2+z^2)
so then would it become (x+y+z)/(x^2+y^2+z^2)? which is r*/r^2?

 

[Fantini]

Remember the gradient is $$\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right).$$ Since we've established $$\frac{\partial f}{\partial x} = \frac{x}{\sqrt{x^2+y^2+z^2}}$$ and likewise for the other partial derivatives, we have $$\nabla f = \frac{(x,y,z)}{\sqrt{x^2+y^2+z^2}} = \frac{{\mathbf r}}{r} = \frac{\widehat{ {\mathbf r}}}{r^2}.$$ :) Hope this helps. What do you mean with 'zbar'?

 

[Patricio Lima]

Remember the gradient is $$\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right).$$ Since we've established $$\frac{\partial f}{\partial x} = \frac{x}{\sqrt{x^2+y^2+z^2}}$$ and likewise for the other partial derivatives, we have $$\nabla f = \frac{(x,y,z)}{\sqrt{x^2+y^2+z^2}} = \frac{{\mathbf r}}{r} = \frac{\widehat{ {\mathbf r}}}{r^2}.$$ :) Hope this helps. What do you mean with 'zbar'?

I did not understand. gradiente (1/r) = - r/ r^3 ??

 

[I like Serena]

I did not understand. gradiente (1/r) = - r/ r^3 ??

Hi Patricio Lima, welcome to MHB, (Wave)

We had here that:
$$\operatorname{grad} \ln\|\mathbf r\| = -\frac{\mathbf r}{r^2}$$
Similarly we can find:
$$\pd {}x \frac 1r = -\frac 1{r^2}\pd r x = -\frac 1{r^2}\pd {} x\sqrt{x^2+y^2+z^2}
= -\frac 1{r^2}\cdot\frac{2x}{2\sqrt{x^2+y^2+z^2}}
= -\frac x{r^3}$$
So that:
$$\operatorname{grad} \frac 1r = -\frac{\mathbf r}{r^3}$$
(Thinking)