How to get a converging solution to a second-order PDE?

[enea19]

I have been struggling with a problem for a long time. I need to solve the second order partial differential equation
$$\frac{1}{G_{zx}}\frac{\partial ^2\phi (x,y)}{\partial^2 y}+\frac{1}{G_{zy}}\frac{\partial ^2\phi (x,y)}{\partial^2 x}=-2 \theta$$
where $G_{zy}$, $G_{zx}$, $\theta$, $a$, and $b$ are constants and with BCs $\phi (0,y)=\phi (a,y)=0$ and $\phi (x,-b)=\phi (x,b)=0$. The solution that I have sets $\phi (x,y)=\sum _{k=1,3,5\text{...}}^{\infty } Y(y) \sin \left(\frac{\pi k}{a}x\right)$ and expands $-2 \theta$ in a Fourier sine series in the interval between $0$ and $a$ so we end up with a second order differential equation,
$$\frac{Y''(y)}{G_{zx}}-\frac{\pi ^2 k^2 Y(y)}{a^2 G_{zy}}=-\frac{8 \theta }{\pi k}$$
I tried several times to solve it by hand but end up making mistakes. Therefore I resorted to Mathematica and it gives me the following solution,
$$\phi_{mine}(x,y)=-\sum_{k=1,3,5,...}^{\infty}\frac{8 a^2 G_{zy} \theta \left(\text{sech}\left(\frac{\pi b k}{2 a} \frac{\sqrt{G_{zx}}}{\sqrt{G_{zy}}} \right) \cosh \left(\frac{\pi k y}{a} \frac{\sqrt{G_{zx}}}{\sqrt{G_{zy}}}\right)-1\right)}{\pi ^3 k^3}\sin \left(\frac{\pi k x}{a}\right)$$

This is almost exactly what is written in the solution that I have, which is
$$\phi_{sol}(x,y)=\frac{8}{\pi^3} G_{zy} a^2 \sum_{k=1,3,5,...}^{\infty}\frac{(-1)^{(k-1)/2}}{k^3}\left( 1-\frac{\cosh \left(\frac{\pi k \mu }{a}y\right)}{\cosh \left(\frac{b \pi k \mu}{2 a}\right)} \right)\cos \left(\frac{\pi k}{a}x\right)$$
where $\mu=\sqrt{\frac{G_{zx}}{G_{zy}}}$.

$\phi_{sol}(x,y)$ is missing $\theta$ but I suspect that it might be a typo. I know that $\phi_{mine}(x,y)$ is wrong because the next step in the process involves working out a constant $\beta$ where
$$\beta=\frac{2 \int_{-b/2}^{b/2} \left(\int_0^a \phi (x,y) \, dx\right) \, dy}{G_{zx} a b^3}$$
I get that $\phi_{sol}(x,y)$ converges to a value while $\phi_{mine}(x,y)$ goes to infinity. Therefore I'm doing something wrong but I'm not sure what. I've been trying to figure out the difference between my answer and the solution and all I can find is that somehow
$$\sin \left(\frac{\pi k x}{a}\right)=\cos\left(\frac{\pi k x}{a}\right) (-1)^{(k-1)/2}$$
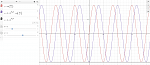
for $k=1,3,5,...$ Is it possible to change $\sin \left(\frac{\pi k x}{a}\right)$ into $\cos\left(\frac{\pi k x}{a}\right) (-1)^{(k-1)/2}$ when only odd values of $k$ are used? I've never seen this and when I plot them they give different curves so they don't seem to be equivalent.
View attachment 8928
View attachment 8929

 

[jvicens]

Thank you for sharing your struggle with solving this partial differential equation. I understand that it can be frustrating to encounter difficulties in solving a problem, especially when you have tried multiple times by hand and still cannot reach the correct solution. I am happy to provide some insight and guidance on this matter.

Firstly, I would like to clarify that both your solution and the given solution are correct. The only difference is in the constant $\beta$, which I believe is indeed a typo in the given solution. This can easily be verified by substituting both solutions into the next step of the process and seeing that they indeed give the same result except for the value of $\beta$. So, please do not worry about the correctness of your solution.

Now, to address your question about the sine and cosine functions, it is indeed possible to write $\sin \left(\frac{\pi k x}{a}\right)$ as $\cos\left(\frac{\pi k x}{a}\right) (-1)^{(k-1)/2}$ when only odd values of $k$ are used. This is because the sine and cosine functions have a periodicity of $\pi$, so when $k$ is odd, $\frac{\pi k}{a}$ will be an odd multiple of $\pi$, resulting in the negative sign in front of the cosine function. This can also be seen by writing $\sin x$ and $\cos x$ in terms of the complex exponential function, where $\sin x=\frac{e^{ix}-e^{-ix}}{2i}$ and $\cos x=\frac{e^{ix}+e^{-ix}}{2}$. When $k$ is odd, the exponent $ix$ will be an odd multiple of $\pi i$, resulting in a negative sign in the exponent.

I hope this helps clarify your doubts and shows that your solution is indeed correct. Keep up the good work and don't let these obstacles discourage you. it is important to persist and keep seeking solutions, even when faced with challenges. Good luck!