How to Maximize an Integral with a Constraint Using Lagrange Multipliers?

[mistergrinch]

I'm trying to find the function f which maximizes this integral:

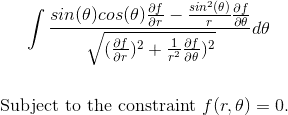
I'm not quite sure how to handle a problem like this with a second variable (r) which is implicitly determined by a constraint. Can anyone help? Thanks.

 

[jvicens]

Hello! I would suggest approaching this problem using the method of Lagrange multipliers. This method is commonly used to maximize a function subject to a constraint. In this case, the constraint would be the implicit function of r.

First, let's define the function f as F(x,r), where x is the variable of integration. Then, we can set up the Lagrangian as L(x,r,λ) = F(x,r) + λ(r - g(x)), where λ is the Lagrange multiplier and g(x) is the implicit function of r.

Next, we can take the partial derivatives of L with respect to x, r, and λ, and set them equal to 0. This will give us a system of equations that we can solve for x, r, and λ.

Once we have the values for x and r, we can plug them back into the original function F(x,r) to find the maximum value of the integral.

I hope this helps! Let me know if you have any further questions.