kelly0303
- 573
- 33
Hello! If I have 2 energy levels split by something of the order of 10 Hz (they can be connected by an electric dipole moment i.e. ##\Delta J = 0## and they have different parities), what would be the best way to measure this difference (even 10% error would be good, but the lower the error the better).
Here is what I have so far with my limited practical experience in spectroscopy: Doing normal Rabi/Ramsey spectroscopy I assume it wouldn't work, as I would need to generate a frequency at ~10Hz, which I don't think it's possible (or is it?). I can in principle still do a Rabi measurement with a detuned frequency, but I assume that the lowest frequency I can generate in practice would still be several orders of magnitude away from 10Hz, so it would take a very long time to populate the excited state enough to have good statistics, so I don't think that would work.
Another thing I can do is to use a Raman like measurement, where the 2 lasers have a frequency difference of 10Hz, but in practice lasers linewidths are much bigger than that, so I am not sure if I could get a good signal from there, i.e. if I can extract the central value with less than 10 Hz error (I don't know much about Raman type measurements, tho). I would appreciate any advice on this and comments on my ideas. Thank you!
Here is what I have so far with my limited practical experience in spectroscopy: Doing normal Rabi/Ramsey spectroscopy I assume it wouldn't work, as I would need to generate a frequency at ~10Hz, which I don't think it's possible (or is it?). I can in principle still do a Rabi measurement with a detuned frequency, but I assume that the lowest frequency I can generate in practice would still be several orders of magnitude away from 10Hz, so it would take a very long time to populate the excited state enough to have good statistics, so I don't think that would work.
Another thing I can do is to use a Raman like measurement, where the 2 lasers have a frequency difference of 10Hz, but in practice lasers linewidths are much bigger than that, so I am not sure if I could get a good signal from there, i.e. if I can extract the central value with less than 10 Hz error (I don't know much about Raman type measurements, tho). I would appreciate any advice on this and comments on my ideas. Thank you!
Last edited by a moderator:
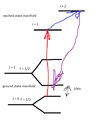
 Good catch, once again! Maybe my first instinct, using the polarization to exclude one parity or the other, is the
Good catch, once again! Maybe my first instinct, using the polarization to exclude one parity or the other, is the