zenterix
- 774
- 84
- TL;DR
- How exactly does this experiment to measure average thermal conductivity of a metallic slab work?
Heat conduction is the transport of energy between neighboring volume elements in a material as a result of the temperature difference between them.
The "fundamental law of heat conduction", as it is called in the book I am reading, is a "generalization of the results of experiments on the linear flow of heat through a slab perpendicular to the faces".
Pictorially, such experiments do the following
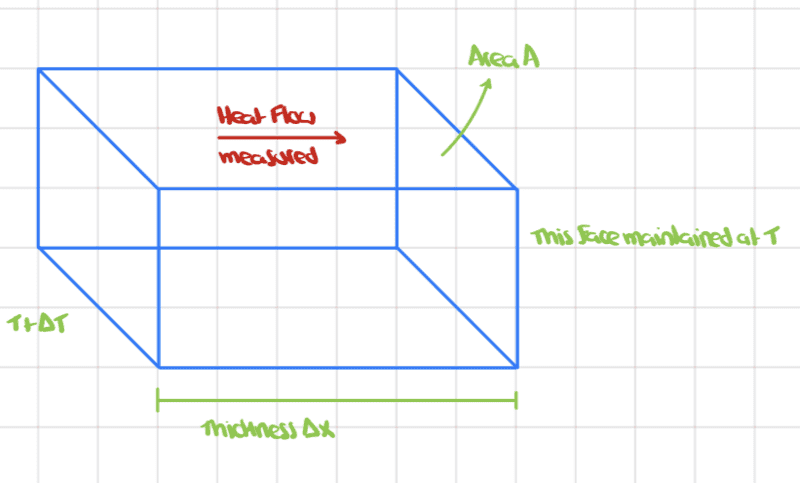
The blue rectangular box represents a slab of a material of thickness ##\Delta x## and the area of the side faces is ##A##. One face is maintained at temperature ##T## and the other at ##T+\Delta T##.
The heat that flows perpendicular to the faces for a time ##t## is measured.
The same experiment is repeated by keeping the material the same and varying ##\Delta x## and ##A##.
These experiments lead to the following result
$$\frac{Q}{t} \propto A\frac{\Delta T}{\Delta x}\tag{1}$$
which is approximately true for finite ##\Delta T## and ##\Delta x## and rigorously true when these are infinitesimals.
In this limit, we obtain
$$\frac{dQ}{dt}=-KA\frac{dT}{dx}\tag{2}$$
where the ##dQ## is an inexact differential (I don't know how to write the correct symbol in latex).
The derivative ##dT/dx## is the temperature gradient, ##K## is the thermal conductivity.
My question is about measurement of thermal conductivity.
Here is the experiment for a metal.
The metal is made into the form of a bar, one end is heated electrically, the other end is cooled with a stream of water. The surface of the bar is thermally insulated.
Heat loss through the insulation is calculated by subtracting the rate at which heat enters the water from the rate at which electrical energy is supplied.
The equation used to determine the average thermal conductivity within the given temperature range is
$$K=\frac{L}{A(T_1-T_2)}\frac{dQ}{dt}\tag{3}$$
where again, ##dQ## is an inexact differential.
The temperature difference is measured with thermocouples at two places a distance ##L## apart.
Here is what I think happens
- The amount of heat provided during a certain time to one end of the metal is known (how does one control the amount of heat?). This is ##dQ/dt##.
- ##L## and ##A## are fixed
- The only thing measured is the "temperature difference". This temperature difference seems to be that between the two metallic faces.
However, it also seems that one somehow measures heat entering the water as well. How does one do this?
Does it involve also measuring the temperature difference of the water?
The "fundamental law of heat conduction", as it is called in the book I am reading, is a "generalization of the results of experiments on the linear flow of heat through a slab perpendicular to the faces".
Pictorially, such experiments do the following
The blue rectangular box represents a slab of a material of thickness ##\Delta x## and the area of the side faces is ##A##. One face is maintained at temperature ##T## and the other at ##T+\Delta T##.
The heat that flows perpendicular to the faces for a time ##t## is measured.
The same experiment is repeated by keeping the material the same and varying ##\Delta x## and ##A##.
These experiments lead to the following result
$$\frac{Q}{t} \propto A\frac{\Delta T}{\Delta x}\tag{1}$$
which is approximately true for finite ##\Delta T## and ##\Delta x## and rigorously true when these are infinitesimals.
In this limit, we obtain
$$\frac{dQ}{dt}=-KA\frac{dT}{dx}\tag{2}$$
where the ##dQ## is an inexact differential (I don't know how to write the correct symbol in latex).
The derivative ##dT/dx## is the temperature gradient, ##K## is the thermal conductivity.
My question is about measurement of thermal conductivity.
Here is the experiment for a metal.
The metal is made into the form of a bar, one end is heated electrically, the other end is cooled with a stream of water. The surface of the bar is thermally insulated.
Heat loss through the insulation is calculated by subtracting the rate at which heat enters the water from the rate at which electrical energy is supplied.
The equation used to determine the average thermal conductivity within the given temperature range is
$$K=\frac{L}{A(T_1-T_2)}\frac{dQ}{dt}\tag{3}$$
where again, ##dQ## is an inexact differential.
The temperature difference is measured with thermocouples at two places a distance ##L## apart.
Here is what I think happens
- The amount of heat provided during a certain time to one end of the metal is known (how does one control the amount of heat?). This is ##dQ/dt##.
- ##L## and ##A## are fixed
- The only thing measured is the "temperature difference". This temperature difference seems to be that between the two metallic faces.
However, it also seems that one somehow measures heat entering the water as well. How does one do this?
Does it involve also measuring the temperature difference of the water?