How to measure the magnification of a microscope in the lab

[JulioHC]

Good evening,

In the following weeks, I will be performing a lab project during three sessions and one of the things that I have to do is to create a microscope using a set of lenses (We are using a 50mm focal length convergent lens as the objective and a 100m focal length convergent lens as the eyepiece). In the last lab session we used to convergent lenses to create a microscope but without taking any readings, now at home I have done some research about microscopes and I have drawn some ray diagrams, I have also derived an equation to calculate the magnification of the system given the two focal lengths, the distance between lenses and the distance from the object to the first lens. The expression that I got is

$$\frac{f_{1}f_{2}}{(s_{1}-f_{1})(d-s_{1}^{'}-f_{2})}$$

Where
- $f_{1},f_{2}$ are the focal lengths of the objective and the eyepiece respectively.
-$s_{1}$ is the distance from the object to the objective.
-$s_{1}^{'}$ is the distance from the objective to the image it creates, which will then be used by the eyepiece to create the final image.

Using these and an online optics simulator I concluded that

- If the lenses are placed so that $f_{2}$ is located to the right of $f_{1}$, the image is smaller than the object.

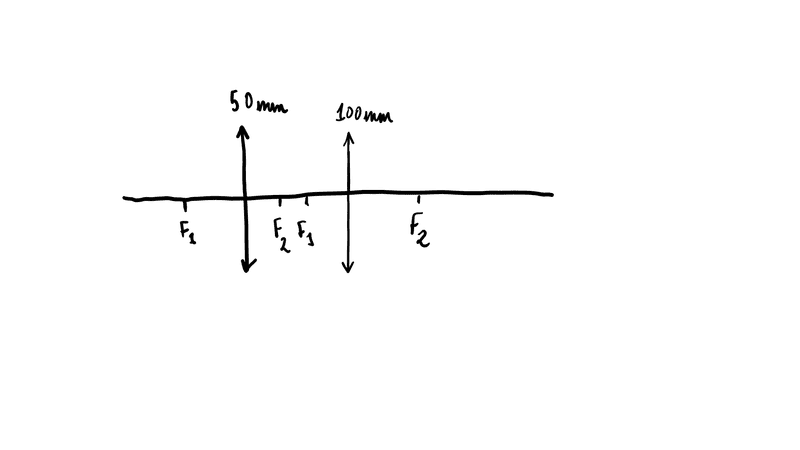
- If the lenses are placed so that $f_{2}$ and $f_{1}$ are at the same place then the magnification is equal to $\frac{f_{2}}{f_{1}}$ no matter where you place the object.

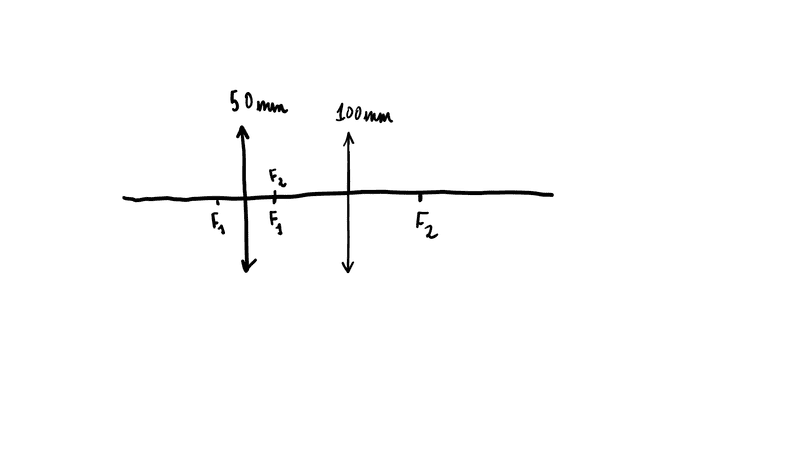
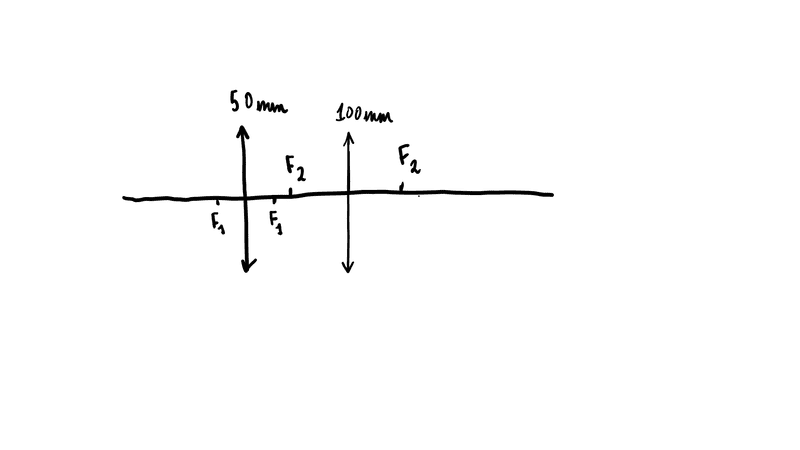
- If the lenses are placed so that $f_{2}$ is to the right of $f_{1}$ the magnification keeps increasing but the image is formed further from the eye piece. My thinking here is that although the magnification increases because the image keeps getting further it must be blurred or not more magnified but I will test this in the lab. Every ray diagram that I have seen on internet shows $f_{2}$ and $f_{1}$ coincident so I assume that $\frac{f_{2}}{f_{1}}$ might be the maximum possible magnification.

Now my question, as I want to test all these conclusions in the lab session I need to figure out a way of measuring experimentally the magnification of the microscope. However, I can't think of any way of doing it given that I can't project the image formed by the microscope as it is virtual. I have been searching online for some procedure to do it but I haven't found anything. That's why I wanted to ask you if you could provide me some help on this matter.

 

[BvU]

It seems to me that, for your calculations, you are assuming a microscope has to form a real image.
If you look (*) through a single lens, say the 50 mm one, would you look at a real image or at a virtual image ?

(*) for magnification, in order to see some detail.

 

[JulioHC]

It seems to me that, for your calculations, you are assuming a microscope has to form a real image.
If you look (*) through a single lens, say the 50 mm one, would you look at a real image or at a virtual image ?

(*) for magnification, in order to see some detail.

Well, it depends on whether we want a real or virtual image. As far as I know, we need the first lens to create a real image on the right of the focal point of the second lens. In this case, the object should be at a distance between f and 2f (One and two focal distances) so that it creates a real magnified image. Then, because it is formed on the right of $f_{2}$ the second lens will create a virtual magnified image of the image created by the first lens.

 

[BvU]

We want to look at the object and see some magnification. So, again: If you look through a single lens, say the 50 mm one, would you look at a real image or at a virtual image ?

 

[JulioHC]

Oh ok, that would be a magnifying glass. In that case, we look at a virtual image.

 

[BvU]

Right. And with a microscope we also want to look at an enlarged image by bringing our eye close to the eyepiece, so the image better be on the other side of the eyepiece lens

Look at the second picture here (the first one is also correct):

Here are two ray diagrams for compound microscope, the first one proposed by the book, and the second one recommended by the teacher:

View attachment 232683

View attachment 232684

In the first image, the light rays form a real image A'B', which becomes the virtual object for the eyepiece. See, the original rays are carried forward to the eyepiece, which then form a virtual image, A"B".

In the second image, when the real image A'B' is formed, new rays start from it, and end up forming the virtual image A''B".

I feel the second one is wrong, because new rays cannot start from a real image, but the original rays should go forth and get refracted again to form the virtual image.

What is your opinion? Which diagram is correct?

 

[BvU]

or here

 

[JulioHC]

Oh, so the first lens creates an enlarged image of the object so that the second lens can use it like a magnifyig glass would and thus creating a virtual image that we can see by looking through the lens. From this I can deduce that the limit of how far I can put the lenses is determined by when the image of the first lens is formed to the left of the focal point of the second lens. Is that right?

 

[BvU]

Almost: as you see in both pictures, the real image is to the right of the focal point of the second lens. Or on top of it -- in the latter case you can look through the eyepiece with unaccommodated eye (As if looking at infinity).
I think you get the idea.

I forgot: my compliments for working this out in advance of the lab time -- an excellent approach !

 

[JulioHC]

Thank you for helping me! Do you mind if I ask you if you know of some procedure that I can use in the lab to measure experimentally the magnification in the lab in order to compare it with the theoretical magnification?

 

[BvU]

Look through the thing with one eye and draw what you see to scale using the other eye ?
(e.g. a mm grid on transparent paper, or something else you know the size of)

 

[JulioHC]

Hi again and thank you for your response!.

At the end I found a quite interesting method to measure the magnification. However, I have now found a problem with our measurements and I'd like to ask the community what they think about my reasoning. The method consists of using a phone to take a picture through the lens and then without moving the phone removing the lenses and taking another picture. Then you transfer the pictures to the computer and using any program that allows you to draw lines over the image and tells you their size you measure two common parts of the object and then divide the length that you measure through the lenses by the length that you measure without the lenses. The problem is that I was just now doing the calculations to compare them to the expected result when none of them was coincident (Not even near) to the expected results. So I think the problem is that we have to calculate the expected angular magnification and not the expected linear magnification because the image and the object are not at the same place. With this in mind, I have decided that we need to take all the measurements again but this time measuring the distance from the second lens to the phone so that we can calculate the expected angular magnification. Once this is done, the method described at the beginning should give the same results for angular magnification. I wanted to ask you if this seems reasonable before doing it before we have limited time and we can't afford to lose another day.

I also wanted to ask about something that happened in the lab and that I don't understand. I derived more equations and one of them gives you the maximum distance between the lenses given the distance of the object to the first lens. If the distance between the lenses if bigger than this maximum distance then the image of the first lens is formed on the left of the focal point of the second lens and the final image is real. I was expecting that if I placed the lenses further than this limit I wouldn't see any image and the microscope just wouldn't work. However, it worked! We could take pictures with the phone and see an image through the lens when according to my knowledge we shouldn't. My assumption is that if I place the lenses further than the limit the system is no longer a microscope but it's something else. However, I don't know what it is and without a name, it's impossible to find more information about how it works, because ray diagrams agree with the prediction that the image is real. If anyone had any information about this I would really appreciate any help.

Have a good day!

 

[JulioHC]

Should I make a new post for this new question?