- #1
rinna
- 1
- 0
Hi , I have been thinking of this question for a long time. Can someone give me an advice?
There are three known matrices M, N, and K.
M is a (4*4) matrix:
M=
[ 1 0 2 3;
2 1 3 5;
4 1 1 2;
0 3 4 3 ]
N is a (4*3) matrix:
N=
[ 3 0 4;
1 5 2;
7 1 3;
2 2 1 ]
K is a (2*4) matrix:
K=
[ 1 0 2 3;
2 1 3 5 ]There is an unknown matrix V, whose size is (3*2).
My question is:
How to minimize the infinity norm of M+NVK and find the V which can minimize the infinity norm of the matrix function? the question formulation is shown in the following:
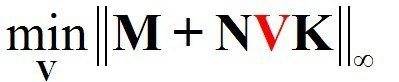
There are three known matrices M, N, and K.
M is a (4*4) matrix:
M=
[ 1 0 2 3;
2 1 3 5;
4 1 1 2;
0 3 4 3 ]
N is a (4*3) matrix:
N=
[ 3 0 4;
1 5 2;
7 1 3;
2 2 1 ]
K is a (2*4) matrix:
K=
[ 1 0 2 3;
2 1 3 5 ]There is an unknown matrix V, whose size is (3*2).
My question is:
How to minimize the infinity norm of M+NVK and find the V which can minimize the infinity norm of the matrix function? the question formulation is shown in the following: