- #1
genxium
- 141
- 2
I'm currently working on a pet project which is similar to the OpenAI Lunar Lander v2 (hence the problem is in a 2D context), and seeking help for a sub-problem that's been blocking me for a while.
At any instant of time, I'm to find
, given
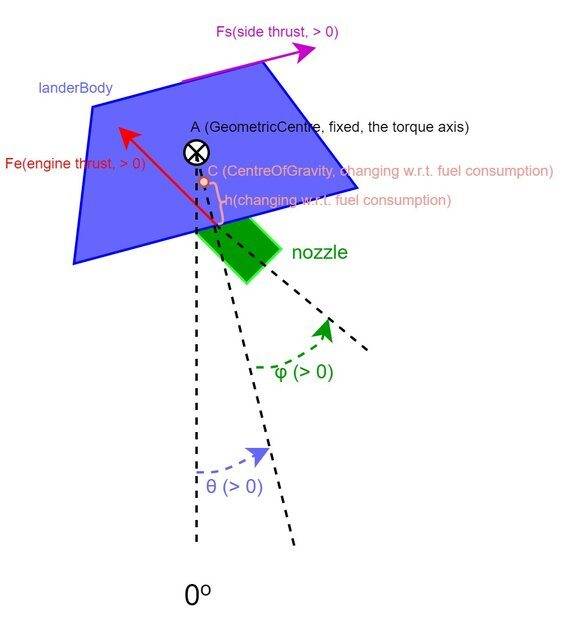
To my understanding, the dynamics are (don't know whether I can use TeX here, tried wrapping with $$ and ## but preview didn't work)
Is there any advice for solving them at least numerically? An analytical solution will certainly be much appreciated but not a pursuit here.
At any instant of time, I'm to find
- Fe: magnitude of main engine thrust, must be >0
- Fs: magnitude of side engine thrust (>0 to point to the "right w.r.t. lander body", and < 0 to point to opposite direction),
- φ: tilted angle of main engine nozzle w.r.t. lander body, should be within [-π/2, +π/2]
, given
- ax: the expected x-acceleration of COG (center of gravity, same below)
- ay: the expected y-acceleration of COG
- βC: the expected angular acceleration w.r.t axis through COG and perpendicular to the plane (this screen)
- m: current mass of the whole lander
- IC: current moment of inertia of the whole lander w.r.t. same axis of βC
- θ: current tilted angle of the lander body w.r.t. the fixed gravity direction
- h: current distance of COG and the nozzle hinge as shown in the figure below
- g: fixed gravity acceleration
- H: total height of the lander body
To my understanding, the dynamics are (don't know whether I can use TeX here, tried wrapping with $$ and ## but preview didn't work)
- -Fe*sin(θ+φ) + Fs*cosθ = ax*m
- Fe*cos(θ+φ) + Fs*sinθ - g*m = ay*m
- Fe*sinφ*h + Fs*(H-h) = βC*IC
Is there any advice for solving them at least numerically? An analytical solution will certainly be much appreciated but not a pursuit here.
Last edited: